Пакет анализа→ Генерация случайных чисел→ Пуассоновское (распределение)

P18 = ПУАССОН (18; 10; 0) ≈ 0,0071

Ещё один вариант решения предоставляет Пакет Анализа:

Пример 4. Завод отправил 5000 доброкачественных изделий. Средняя вероятность того, что в пути разбили одно изделие, равна 0,0002. Найти вероятность того, что в пути будет повреждено: а) 3 изделия, б) 1 изделие, в) не более трех изделий.

Решение. 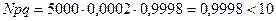и 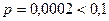, поэтому применяем формулу Пуассона, где .

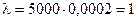а) При : , .

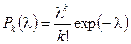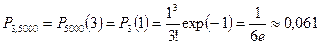б) При :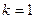

в) Предварительно подсчитаем 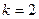: и

: .

.

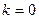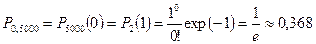Распределение c² или распределение Пирсона

Распределением c² (хи-квадрат) или распределением Пирсона называется распределением суммы квадратов «k» независимых случайных величин, распределённых по стандартному нормальному закону N (0;1), т.е.

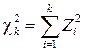
При k = 2 и k = 3 величина c² имеет простой геометрический смысл.

Свойства распределение Пирсона

· .

·

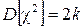
· С возрастанием числа степеней свободы «k» распределение c² медленно приближается к нормальному закону распределения, а при k >30 оно близко к стандартному нормальному закону распределения.

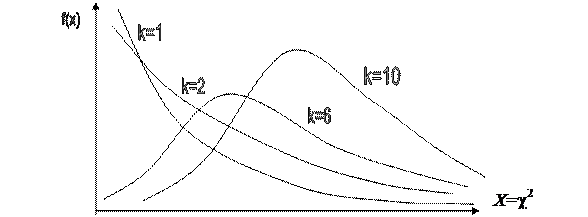
t – Распределение или распределение Стьюдента

Student – псевдоним английского статистика Госсета (1876-1937)

t – Распределением называется распределение случайной величины

,

где Z, Z ₁,…, Z_n – независимые случайные величины, распределённые по стандартному нормальному закону N (0;1). Для t – распределения, как и для распределения N (0;1) — .

Замечание. При n > 30 случайная величина t имеет распределение N (0;1).

, , , .

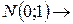
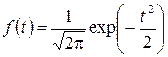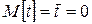Практические примеры

Пример 5. Интервальная оценка математического ожидания (использование t – распределения). Пусть имеется выборка случайных величин «x» объёмом «n». Подсчитаем среднее 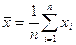и несмещенную дисперсию . Требуется определить доверительный интервал математического ожидания «а» генеральной совокупности по случайной выборке объёмом «n».

Решение. Введем случайную величину

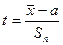, где 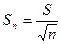– стандартная ошибка среднего.

Случайная величина «t» подчиняется распределению Стьюдента, причем

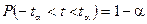, где a – уровень значимости.

Тогда

,

.

Величину 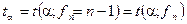проще всего рассчитать с использованием стандартных функций EXCEL, а именно

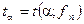= СТЬЮДРАСПОБР().

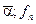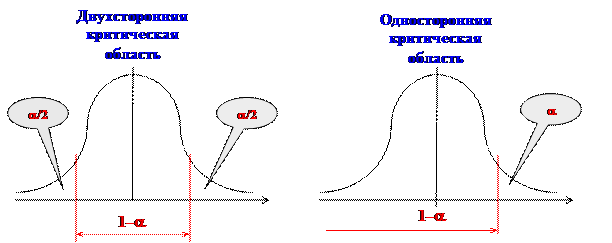
В зависимости от конкурирующей гипотезы, для обоснования критерия выбирают одностороннюю или двухстороннюю критические области, при этом в первом случае 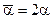, во втором – 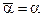. Т.е.

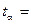СТЬЮДРАСПОБР(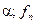) – для двухсторонней критической области,

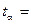СТЬЮДРАСПОБР() – для односторонней критической области.

Пример 6. Вторым важным применением t –критерия является возможность оценки значимости линейного коэффициента корреляции

.

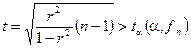Пример 7. При случайная величина «t» имеет распределение близкое к нормальному N (0;1). В этом случае интервальная оценка для среднего существенно упрощается

.

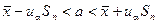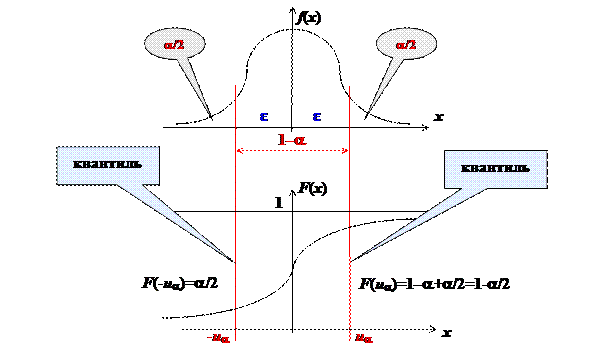
Здесь – двухсторонние критические границы для нормального распределения N (0;1) (квантили), отвечающие условию .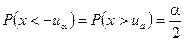

Дата добавления: 2013-12-13