Статистическое изучение взаимосвязей социально-экономических явлений

1. Виды и формы связей между явлениями.

2. Методы изучения взаимосвязей.

3. Корреляционно-регрессионное моделирование.

4. Оценка КРМ на адекватность.

1. Все явления объективного мира, в том числе и общественные, находятся в постоянной взаимосвязи и взаимодействии между собой, в непрерывном изменении и развитии. Важнейшей задачей статистики, наряду с оценкой состояния массовых явлений и выявлением закономерностей их развития, является изучение связей между ними.

Связи массовых общественных явлений устанавливают на основе теоретического анализа их сущности, изучения закономерностей и движущих сил развития, оценки условий их функционирования. При этом используются категории, понятия и накопленные ранее знания других наук. Задача статистики состоит в том, чтобы выявить само наличие связи в конкретных условиях, а также получить показатели, характеризующие ее силу, степень и характер.

Теоретический и практический интерес представляют в первую очередь причинно-следственные связи, когда одни явления (факторы) выступают причиной изменения других (результаты). Их анализ позволяет, во-первых, объяснить фактическое положение дел, а во-вторых, воздействуя на факторы, добиться изменения результатов в желаемом направлении.

Виды связей:

I. По характеру:

1) функциональные. Связь между явлениями называется функциональной, если изменению факторного показателя x на единицу соответствует строго определенное изменение результативного признака y. Такие связи выражают формулами, действительными во всех случаях. Примером может служить изменение заработной платы (при той же самой часовой ставке) в зависимости от числа отработанных часов, изменение затрат на топливо в зависимости от его расхода в натуральном выражении (при неизменных ценах) и т.д.

2) статистические (корреляционные). Статистическими (корреляционными) называют связи, при которых строго определенному изменению факторного признака x соответствует целый ряд (статистическое распределение) изменений результата y, не вполне определенных, подверженных случайным колебаниям. Эти связи проявляются лишь в среднем, в массовых явлениях; кроме изучаемого фактора на результат воздействуют и другие причины, в том числе носящие случайный характер. Например, при увеличении доз вносимых удобрений урожайность культур в среднем повышается, но не всегда и не на одну и ту же величину.

II. По форме выражения:

1) прямые - с возрастанием факторного признака увеличивается результативный (например, при увеличении стажа работника, как правило, производительность его труда повышается);

2) обратные - изменения идут в противоположном направлении (так, при повышении продуктивности животных и урожайности культур затраты на единицу продукции в среднем сокращаются).

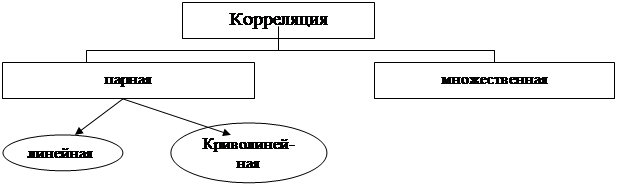
III. По аналитическому выражению:

1) прямолинейные - с возрастанием одного признака при любом его исходном значении другой изменяется в среднем на одну и ту же величину;

2) криволинейные - эти изменения сами изменяются (увеличиваются, уменьшаются или даже меняют свой знак).

IV. В зависимости от количества факторных признаков, включенных в модель:

1) парные (однофакторные);

2) множественные (многофакторные).

2. Для изучения функциональных связей используют методы:

- балансовые связи. Он основан на простой функциональной зависимости между наличием какого-то ресурса на начало и конец периода, его поступлением и расходованием в течение этого периода. Если известны любые три из указанных показателей, четвертый определяется автоматически. Наличие на конец года = Наличие на начало года + Поступило – Выбыло.

Например, годовое потребление в хозяйстве продукции собственного производства можно рассчитать так:

Потребление = Наличие на начало года + Производство – Наличие на конец года.

- индексного анализа.

Для изучения корреляционных связей используют методы:

- сопоставление параллельных рядов;

Самый простой и наиболее распространенный прием – сопоставление параллельных рядов. Его сущность состоит в одновременном рассмотрении изучаемых признаков по единицам совокупности или по периодам (моментам) динамического ряда. Сопоставление производится чисто визуально, без специальных расчетов (табл 9.3).

В данном случае хорошо видно, что в динамике дозы внесения органических и минеральных удобрений вплоть до 1990 г. увеличиваются, а затем снижаются. Сходная тенденция наблюдается и по урожайности зерновых: рост до 1990 г. с последующим снижением. Напротив, по урожайности картофеля никакого параллелизма с показателями внесения удобрений не прослеживается.

Сопоставление параллельных рядов (его особенно удобно вести с помощью линейных графиков) позволяет установить наличие связи, ее направление и очень приблизительно – ее силу. Так, изменения доз органических и минеральных удобрений связаны очень тесно, их связь с урожайностью зерновых культур, хотя и слабая, также имеется, она носит прямой и линейный характер, а вот связь с урожайностью картофеля практически не прослеживается.

Главный недостаток данного приема – отсутствие каких-либо показателей связи. Сопоставление не решает также вопрос о причинно-следственных связях изучаемых явлений. Из теории, например, известно, что внесение удобрений приводит к росту урожайности. Но картофель возделывается в основном в хозяйствах населения, и его доля в структуре посевов невелика. Поэтому показатель внесения удобрений в среднем на 1 га всей посевной площади, и к тому же во всех категориях хозяйств, является слишком общим, чтобы могла обнаружиться какая-то связь с урожайностью картофеля.

- графический метод (метод корреляционного поля);

Состоит в нанесении точек графика на координатную плоскость, а также определении поля корреляции и направления связи между признаками.

Пример: Имеются данные:

Урожайность, ц/га	Количество внесенных удобрений на 1 га посевов, т.
	2,6
	2,6
	2,7
	3,0
	2,7

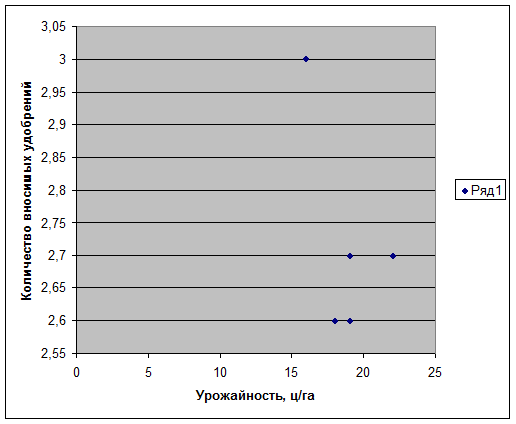
Обратная зависимость.

- метод построения групповых корреляционных таблиц;

Имеются данные:

Стаж, лет х	Выработка одного работника, шт. у

/

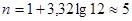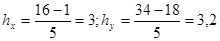
Границы групп для х:

1 гр.: 1-4;

2 гр.: 4-7;

3 гр.: 7-10;

4 гр.: 10-13;

5 гр.: 13-16.

Границы групп для у:

1 гр.: 18-21,2;

2 гр.: 21,2-24,4;

3 гр.: 24,4-27,6;

4 гр.: 27,6-30,8;

5 гр.: 30,8-34.

Таблица – Групповая корреляционная таблица

х	18-21,2	21,2-24,4	24,4-27,6	27,6-30,8	30,8-34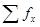
1-4		-	-	-	-
4-7			-	-	-
7-10	-			-	-
10-13	-	-		-	-
13-16	-	-		-
				-

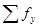
Вывод: связь прямая однонаправленная (т.к. частоты расположены по диагонали).

- метод аналитических группировок;

- метод дисперсионного анализа;

- метод КРА;

- метод непараметрической оценки связей.

3. Метод корреляционно-регрессионного моделирования состоит из двух этапов:

I. Регрессия – поиск уравнения связи, которое наиболее полно характеризует зависимость между признаками, и определение параметров этого уравнения.

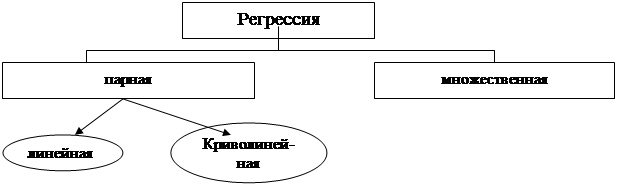
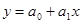
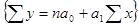
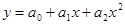
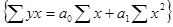
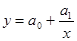
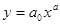
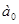- условное начало, содержательной интерпретации не подлежит;

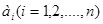- коэффициенты регрессии, показывающие, на сколько единиц изменится результативный признак при изменении факторного признака на единицу при улови, что все прочие факторные признаки останутся неизменными.

II. Корреляция – определение показателей тесноты связи.

Чаще всего корреляцию характеризуют двумя показателями:

- коэффициент корреляции (характеризует степень тесноты связи между результативным и всеми факторными признаками; измеряется в интервале от 0 до 1 по модулю; чем ближе к 1, тем более тесная связь между признаками);

- коэффициент детерминации (показывает, на сколько процентов включенные в модель факторы объясняют вариацию результативного признака: измеряется в интервале от 0 до 100%).

1. Коэф. парной корреляции 1. Индекс корреляции 1. Множеств. коэф.

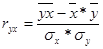
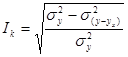корреляции

2. Коэф. парной детерминации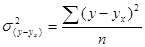

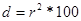
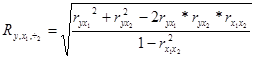
2. Эмперический коэф. детерми-

нации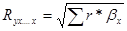

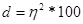
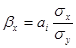
2. Коэф. множ. детерминации

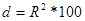
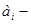коэффициент чистой регресс при i- том факторном признаке;

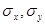- ср. кВ. отклонения по i-тому факторному признаку.

Чтобы сделать коэффициенты регрессии сопоставимыми и определить влияние каждого в отдельности фактора на результативный признак, рассчитывают стандартизированные коэффициенты:

1) Коэффициенты эластичности:

.

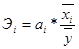Коэффициенты эластичности показывают, на сколько процентов изменится результативный признак, при увеличении факторного признака на 1%.

2)

.

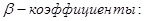
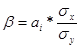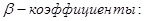показывают, на сколько средний квадратических отклонений изменится результативный признак при увеличении факторного на свое среднее квадратическое отклонение.

3) Коэффициенты отдельного определения:

.

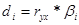Коэффициенты отдельного определения определения показывают вклад каждого фактора в вариацию результативного признака.

4. Адекватность КРМ – это оценка построенной модели в действительности.

Оценка построенной модели на адекватность проводится с использованием F критерия Фишера:

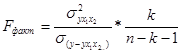, где

n – объем совокупности;

k – число факторных признаков в уравнении;

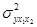- дисперсия выровненных значений результативного признака по уравнению регрессии.

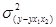- дисперсия отклонений фактических значений результативного признака от выровненных по уравнению регрессии.

По таблице значений F- критерия Фишера определяется табличное его значение при уровне значимости 0,01; 0,05; или 0,1 и числе степеней свободы n-k-1. Если 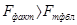- модель адекватна.

Значимость коэффициентов регрессии определяется с помощью критерия Стьюдента.

Дата добавления: 2013-12-13