
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклади розв’язання задач
|
|
|
|
Прямолінійні твірні поверхонь другого порядку.
Поверхні обертання.
Поняття конічної поверхні. Рівняння конічних поверхонь.
Поняття циліндричної поверхні. Рівняння циліндричних поверхонь. Приклади.
План.
Циліндричні та конічні поверхні. Поверхні обертання. Прямолінійні твірні поверхонь другого порядку.
Лекція 17
1. Нехай у просторі задана деяка лінія 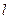 та вектор
та вектор  , який задає певний напрям.
, який задає певний напрям.
Означення 1. Множину всіх прямих, які перетинають задану лінію та паралельні даному напряму, називають циліндричною поверхнею.
Для того, щоб скласти рівняння такої поверхні в деякій афінній системі координат, вважатимемо, що лінія 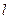 задана системою рівнянь
задана системою рівнянь
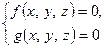 , (1)
, (1)
 тобто задана, як лінія перетину двох поверхонь, а вектор
тобто задана, як лінія перетину двох поверхонь, а вектор  заданий своїми координатами:
заданий своїми координатами:  . Нехай точка
. Нехай точка  належить циліндричній поверхні. Проведемо через неї у напрямку вектора
належить циліндричній поверхні. Проведемо через неї у напрямку вектора  пряму, яка перетне лінію
пряму, яка перетне лінію 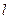 у деякій точці
у деякій точці 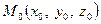 , (рис. 1). Очевидно, що вектори
, (рис. 1). Очевидно, що вектори  та
та  будуть колінеарні. З рівності
будуть колінеарні. З рівності 
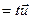 дістаємо співвідношення, які зв’язують координати векторів:
дістаємо співвідношення, які зв’язують координати векторів:
 . (2)
. (2)
Оскільки точка 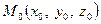 належить лінії
належить лінії 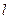 , то виконуються рівності
, то виконуються рівності
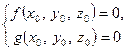 . (3)
. (3)
Підставляючи рівності (2) в (3), дістаємо  . Одержані співвідношення містять змінний параметр
. Одержані співвідношення містять змінний параметр 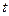 , виключаючи який із системи, дістаємо деяку рівність
, виключаючи який із системи, дістаємо деяку рівність 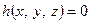 , яка зв’язує змінні
, яка зв’язує змінні  та
та 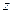 і є шуканим рівнянням циліндричної поверхні. Лінію
і є шуканим рівнянням циліндричної поверхні. Лінію 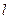 називають напрямною, а прямі, які перетинають
називають напрямною, а прямі, які перетинають 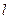 та мають напрям вектора
та мають напрям вектора  - твірними циліндричної поверхні.
- твірними циліндричної поверхні.
Користуючись наведеним алгоритмом, складемо рівняння циліндричної поверхні, напрямною якої є лінія, що лежить в площині  та має рівняння
та має рівняння  , а твірні паралельні до осі
, а твірні паралельні до осі  . Рівності (2) у цьому випадку матимуть вигляд
. Рівності (2) у цьому випадку матимуть вигляд 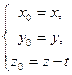 . Підставляючи їх у систему
. Підставляючи їх у систему  , дістаємо рівняння циліндричної поверхні
, дістаємо рівняння циліндричної поверхні  , яке, як бачимо, співпадає з рівнянням лінії. Вибираючи в ролі напрямних лінії другого порядку: еліпс (зокрема коло), гіперболу та параболу, дістаємо три види поверхонь другого порядку, які є частинними випадками циліндричних поверхонь:
, яке, як бачимо, співпадає з рівнянням лінії. Вибираючи в ролі напрямних лінії другого порядку: еліпс (зокрема коло), гіперболу та параболу, дістаємо три види поверхонь другого порядку, які є частинними випадками циліндричних поверхонь:



 - еліптичний циліндр (зокрема
- еліптичний циліндр (зокрема 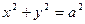 - круговий циліндр) (рис.
- круговий циліндр) (рис.  ),
), 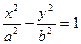 - гіперболічний циліндр (рис.
- гіперболічний циліндр (рис.  ) та
) та 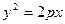 - параболічний циліндр (рис.
- параболічний циліндр (рис. 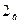 ).
).
2. Нехай у просторі задана деяка лінія 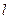 та точка
та точка 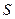 .
.
Означення 2. Множину всіх прямих, які перетинають задану лінію 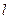 та проходять через дану точку
та проходять через дану точку 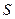 , називають конічною поверхнею.
, називають конічною поверхнею.
Виведемо рівняння конічної поверхні, вважаючи, що лінія 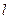 задана системою рівнянь
задана системою рівнянь 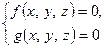 , а точка
, а точка 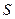 задана своїми координатами:
задана своїми координатами: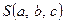 . Нехай точка
. Нехай точка  належить конічній поверхні. Проведемо через неї та точку
належить конічній поверхні. Проведемо через неї та точку 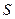 пряму, яка перетне лінію
пряму, яка перетне лінію 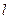 в деякій точці
в деякій точці 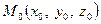 (рис. 3).
(рис. 3).
 Очевидно, що вектори
Очевидно, що вектори  та
та  будуть колінеарні. З рівності
будуть колінеарні. З рівності 
 дістаємо співвідношення, які зв’язують координати векторів:
дістаємо співвідношення, які зв’язують координати векторів:
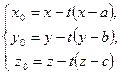 . (4)
. (4)
Оскільки точка 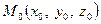 належить лінії
належить лінії 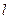 , то виконуються рівності
, то виконуються рівності 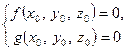 , підставляючи в які співвідношення (4), дістаємо
, підставляючи в які співвідношення (4), дістаємо  . Виключаючи з одержаних рівностей змінний параметр
. Виключаючи з одержаних рівностей змінний параметр 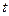 , дістаємо рівність
, дістаємо рівність 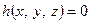 , яка і є рівнянням конічної поверхні. Лінію
, яка і є рівнянням конічної поверхні. Лінію 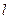 називають напрямною, прямі, які перетинають
називають напрямною, прямі, які перетинають 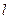 та проходять через точку
та проходять через точку 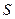 - твірними, а точку
- твірними, а точку 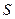 - вершиною конічної поверхні.
- вершиною конічної поверхні.
 Складемо рівняння конічної поверхні, напрямною якої є лінія
Складемо рівняння конічної поверхні, напрямною якої є лінія 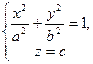 , тобто еліпс, розташований в площині
, тобто еліпс, розташований в площині 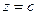 , а вершина
, а вершина 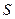 знаходиться в початку координат. Нехай точка
знаходиться в початку координат. Нехай точка  належить конічній поверхні, а точка
належить конічній поверхні, а точка 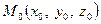 належить заданій напрямній та променю
належить заданій напрямній та променю  . З векторної рівності
. З векторної рівності  дістаємо
дістаємо  . Підставивши одержані співвідношення у систему
. Підставивши одержані співвідношення у систему 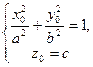 , отримуємо
, отримуємо  , звідки, виключаючи параметр
, звідки, виключаючи параметр 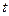 , дістаємо
, дістаємо
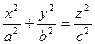 . (5)
. (5)
Одержане рівняння є рівнянням шуканої конічної поверхні. При  напрямна
напрямна 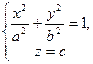 буде колом, а рівняння (5) зведеться до виду
буде колом, а рівняння (5) зведеться до виду
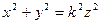 .
.
Це рівняння задає поверхню другого порядку, яку називають круговим конусом (рис. 4).
3. Перейдемо до розгляду поверхонь, які утворюються при обертанні деякої лінії навколо певної прямої. Вважатимемо, що лінія та пряма лежать в одній площині. Такі поверхні називаються поверхнями обертання.
Нехай в площині  рівнянням
рівнянням  , де
, де 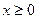 , задана деяка лінія
, задана деяка лінія 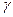 . Розглянемо поверхню, утворену в результаті її обертання навколо осі
. Розглянемо поверхню, утворену в результаті її обертання навколо осі  (рис.5).
(рис.5).
 Нехай точка
Нехай точка  належить поверхні. Проведемо через неї площину перпендикулярно до осі
належить поверхні. Проведемо через неї площину перпендикулярно до осі  , яка перетне вісь
, яка перетне вісь  в деякій точці
в деякій точці 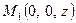 , а також лінію
, а також лінію 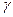 у точці
у точці 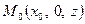 . Оскільки
. Оскільки 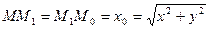 та
та  , то
, то
 . (5)
. (5)
Одержана рівність виражає зв'язок між змінними  та
та 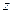 , тому є рівнянням шуканої поверхні. При
, тому є рівнянням шуканої поверхні. При 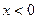 дістаємо
дістаємо  , тому рівність (5) залишається вірною, тобто рівняння (5) в усіх випадках є рівнянням шуканої поверхні обертання.
, тому рівність (5) залишається вірною, тобто рівняння (5) в усіх випадках є рівнянням шуканої поверхні обертання.
Наведемо приклади поверхонь обертання. Нехай в площині  задана пряма
задана пряма  . При її обертанні навколо осі
. При її обертанні навколо осі  дістаємо поверхню, яка задається рівнянням
дістаємо поверхню, яка задається рівнянням  , тобто є конусом. При обертанні навколо осі
, тобто є конусом. При обертанні навколо осі  прямої
прямої  дістаємо круговий циліндр
дістаємо круговий циліндр 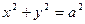 . Обертання еліпса
. Обертання еліпса 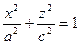 , гіперболи
, гіперболи  , або параболи
, або параболи 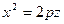 навколо осі
навколо осі  приводить нас до рівнянь
приводить нас до рівнянь  ,
, 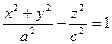 та
та  відповідно, які, як нам уже відомо, виражають еліпсоїд, гіперболоїд та параболоїд обертання.
відповідно, які, як нам уже відомо, виражають еліпсоїд, гіперболоїд та параболоїд обертання.
4. Введемо поняття прямолінійних твірних поверхонь другого порядку.
Означення 3. Пряму, кожна точка якої належить поверхні, називають прямолінійною твірною цієї поверхні.
Очевидно, що кожна твірна циліндричної та конічної поверхні є її прямолінійною твірною. Дослідимо питання існування прямолінійних твірних у випадку інших поверхонь. Не розглядаючи поверхні еліпсоїда, двопорожнинного гіперболоїда та еліптичного параболоїда, для яких, очевидно, прямолінійних твірних не існує, зупинимось на випадку однопорожнинного гіперболоїда. Розглянемо його канонічне рівняння  , яке запишемо у виді
, яке запишемо у виді
 . (6)
. (6)
Крім цього розглянемо системи рівнянь
 (7)
(7)
та
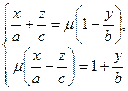 , (8)
, (8)
де  та
та  - довільні числові параметри. Кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Оскільки дві довільні площини з кожної системи перетинаються, то обидві системи задають
- довільні числові параметри. Кожне з рівнянь систем є рівнянням першого степеня, тобто визначає в просторі деяку площину. Оскільки дві довільні площини з кожної системи перетинаються, то обидві системи задають  - та
- та  - параметричні множини прямих. Очевидно, що кожний розв’язок систем (7) та (8) задовольняє рівняння (6), тому ці системи задають
- параметричні множини прямих. Очевидно, що кожний розв’язок систем (7) та (8) задовольняє рівняння (6), тому ці системи задають  - та
- та  - параметричні сім’ї прямолінійних твірних однопорожнинного гіперболоїда.
- параметричні сім’ї прямолінійних твірних однопорожнинного гіперболоїда.
Будемо вважати, що системи (7) та (8) містять, як частинні випадки, рівняння прямих  та
та  . Їх не можна отримати із даних систем при будь-яких скінчених значеннях параметрів
. Їх не можна отримати із даних систем при будь-яких скінчених значеннях параметрів  - та
- та  , але можна розглядати, як результат граничного переходу в системах
, але можна розглядати, як результат граничного переходу в системах 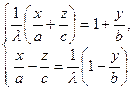 та
та  при
при  та
та 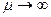 .
.
Доведемо наступне твердження.
Теорема. Через кожну точку однопорожнинного гіперболоїда проходить рівно по одній прямій з кожної  - та
- та  - параметричних сімей прямих (7) та (8). Дві довільні прямолінійні
- параметричних сімей прямих (7) та (8). Дві довільні прямолінійні
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 3903; Нарушение авторских прав?; Мы поможем в написании вашей работы!