ЗДР першого порядку. Диференціальне рівняння називається звичайним (ЗДР), якщо невідома функція є функцією однієї змінної

ЗДР вищого порядку.

7.5. Контрольні запитання.

Диференціальне рівняння називається звичайним (ЗДР), якщо невідома функція є функцією однієї змінної, і диференціальним рівнянням в частинних похідних, якщо невідома функція є функцією багатьох змінних.

Таким чином, звичайним диференціальним рівнянням називають рівняння виду:

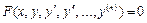, (1)

де x – незалежна змінна; y = y(x) – невідома функція; 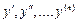¾ відповідно похідні цієї функції порядку 1, 2,…, n.

Розв’язком диференціального рівняння (1) на деякому інтервалі (a;b) називається диференційована на цьому інтервалі функція y = y(x), яка при підстановці в рівняння (1) перетворює його в тотожність по x на (a;b).

Кожне диференціальне рівняння має безліч розв’язків. Щоб знайти частинний розв’язок рівняння необхідно, задати додаткові умови. Залежно від способу задання додаткових умов розрізняють два типи задач: задача Коші і крайова задача.

Якщо додаткові умови задаються в одній точці, то така задача називається задачею Коші, а ці умови ¾ початковими умовами.

Якщо додаткові умови задаються більш ніж в одній точці, то така задача називається крайовою задачею, а умови ¾ крайовими або граничними.

Задача Коші полягає в тому, щоб знайти розв’язок y(x) звичайного диференціального рівняння першого порядку

, (2)

який задовольняє початкову умову

. (3)

З погляду геометрії розв’язати задачу Коші ¾ це означає виділити з множини інтегральних кривих (розв’язків) ту, яка проходить через задану точку .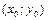

Для розв’язання задачі Коші широко використовують чисельні методи, які дають наближений розв’язок диференціального рівняння у вигляді таблиці значень. В основі цих методів лежить покроковий принцип визначення шуканої функції. Найпоширенішими є методи Ейлера та Рунге – Кутта.

В курсі вищої математики доводять теореми про існування та єдиність розв’язку в залежності від тих чи інших умов. Розглянуті два типи задач можна розв’язати за допомогою MathCAD:

o Задачі Коші – для яких визначені початкові умови для шуканих функцій, тобто задані значення цих функцій в початковій точці інтервалу інтегрування рівняння;

o Крайові задачі – для яких задані деякі відношення зразу на обох границях інтервалу.

В більшості випадків диференціальне рівняння можна записати в стандартному вигляді y'(х)=f(х, y(х)). І тільки з такою формою запису рівняння вміє працювати обчислювальний процесор MathCAD.

7.2. Обчислювальний блок Given/Odesolve.

Обчислювальний блок для рішення одного ЗДР, що реалізує чисельний метод Рунге-Кутта, складається із трьох частин:

o Given – ключове слово;

o ЗДР і початкові умови, записані за допомогою логічних операторів (початкова умова повинна бути записана у вигляді );

o Odesolve (x,x1) – вбудована функція для рішення ЗДР відносно змінної х на інтервалі (х0, х1).

Приклад №1. Розглянемо розв’язання задачі математичної екології, яка описує динаміку популяції з внутрішньою конкуренцією. Спочатку виникає ріст чисельності популяції, близький до експоненціального, а потім вихід на стаціонарнийстан. Рівняння, що описує цей процес має вигляд .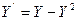

Знайдемо розв’язок

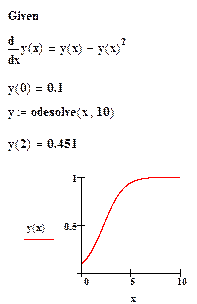
MathCAD вимагає, щоб кінцева точка інтегрування ЗДР лежала правіше початкової, тобто х0<x1. Як можна зауважити, результатом використання блоку Given/Odesolve є функція у(х), визначена на проміжку (х0,х1). Потрібно скористатися звичайними засобами MathCAD, щоб побудувати її графік або отримати значення функції в будь-якій точці вказаного інтервалу, наприклад у(2)=0.451.

Користувач має можливість вибрати між двома модифікаціями чисельного метода Рунге-Кутта. Для зміни методу необхідно клацнути правою кнопкою миші на області функції Odesolve, визвати контекстне меню і вибрати в ньому один з двох пунктів Fixed (фіксований крок) або Adaptive (адаптивний). За замовчуванням приміняться перший з них.

7.3. Вбудовані функції rкfixed, Rkadapt, Bulstoer.

Чисельні рішення задачі Коші для диференціальних рівнянь і систем рівнянь можуть бути реалізовані функціями:

o rkfixed(y,x1,x2,n,F) - повертає матрицю рішень системи диференціальних рівнянь методом Рунге-Кутта 4-го порядку при фіксованому кроці по x.

o rkadapt(y,x1,x2,n,F) - шукає рішення зі змінним кроком (там, де рішення змінюється повільніше, крок збільшується, а в області швидкої зміни рішення крок функції зменшується). Функція працює швидше, ніж rkfixed.

o Bulstoer(y,x1,x2,n,F) - дає більш точне рішення (методом Bulirsch-Stoer).

Де:

o y - вектор початкових умов;

o x1,x2 - границі інтервалу для пошуку рішення;

o n - кількість точок на інтервалі;

o F(x,y) - вектор-функція перших похідних.

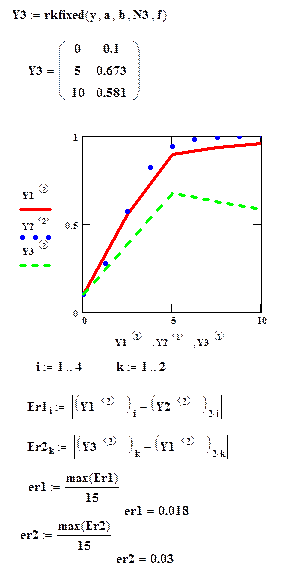
Приклад №2. Розглянемо рішення задачі математичної екології за допомогою вбудованої функції rкfixed.

Дата добавления: 2013-12-13