Числовые характеристики простейшего потока

Распределение числа событий на интервале времени

Можно показать, что вероятность появления ровно k событий на интервале времени t определяится т. н. распределением Пуассона:

.

Математическое ожидание интервала времени между соседними событиями

.

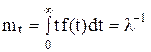Дисперсияинтервалов времени между событиями

.

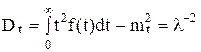(вопрсы: что такое m и D)

среднее квадратическое отклонение s_t= l^-1. Равенство математического ожидания и среднего квадратического отклонения характерно для экспоненциального распределения и может быть использовано для проверки статистической гипотезы о распределении интервалов времени между событиями.

Математическое ожидание числа событий за время t можно определить из распределения Пуассона [12]. Как и следовало ожидать,

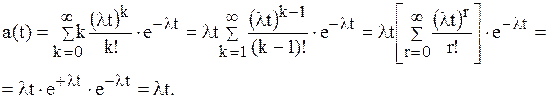
Найдем вероятность того, что событие не наступит на интервале времени t при условии, что перед этим событие не наступало в течение некоторого времени t. Эта вероятность равна вероятности того, что событие не наступит в течение всего интервала времени t+t, то есть p₀(t+t). С другой стороны, эта же вероятность равна произведению p₀(t)×p₀(t/t), где p₀(t/t) - это условная вероятность того, что событие не наступит в течение интервала времени t при условии, что событие не наступило в течение предшествующего интервала времени t. Следовательно,

p₀(t+t) = p₀(t) p₀(t/t).

Тогда условная вероятность

.

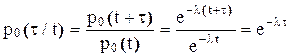Таким образом, показано, что в простейшем потоке отсутствует последействие то есть вероятность того, что в течение интервала t событие не наступит (а, следовательно, и вероятность противоположного события) не зависит от того, сколько времени прошло с момента наступления предыдущего события, а зависит только от протяженности самого интервала t.

Иными словами, если заявки давно не было, это не значит, что она скоро появится и, наоборот, если заявка появилась недавно, это не значит, что следующей долго не будет. Вероятность отсутствия заявки остается неизменной и равной p₀(t)=e^-lt , а математическое ожидание времени до ее появления остается равным 1/l, начиная с любой точки отсчета времени.

Дата добавления: 2013-12-13