Логический синтез вычислительных схем

Рассмотрим логический синтез (создание) вычислительных схем на примере одноразрядного двоичного сумматора, имеющего два входа (″а″ и ″b″) и два выхода (″S″ и ″P″) и выполняющего операцию сложения в соответствии с заданной таблицей:

a	b	f 1(a,b)=S	f 2(a,b)=P

где f ₁(a,b)=S – значение цифры суммы в данном разряде;

f ₂(a,b)=P – цифра переноса в следующий (старший) разряд.

Согласно соотношению (2), можно записать:

S=ƒ₁(a,b)=0*a*b+1*a*b+1*a*b+0*a*b=a*b+a*b;

P=ƒ₂(a,b)=1*a*b+0*a*b+0*a*b+0*a*b=a*b.

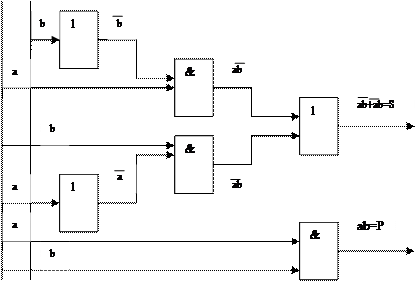
Логическая схема сумматора, реализующего полученную функцию, представлена на рис. 1.1

Рис 1.1 Логическая схема сумматора

Здесь изображены логические блоки в соответствии с международным стандартом:

Схема ИЛИ, реализующая операцию логического сложения

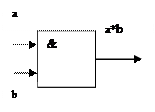
Схема И, реализующая операцию логического умножения

Схема НЕ, реализующая операцию инверсия

Прмечание: 1. В ряде случаев перед построением логической схемы устройства по логической функции последнюю, пользуясь соотношениями алгебры логики, следует преобразовать к более простому виду (минимизировать).

2.Для логических схем ИЛИ,И и НЕ существуют типовые технические схемы, реализующие их на реле, электронных лампах, дискретных полупроводниковых элементах. Для построения современных ЭВМ обычно применяются системы интегральных элементов, у которых с целью большей унификации в качестве базовой логической схемы используются всего одна схема: И – НЕ (штрих Шеффера), ИЛИ – НЕ (стрелка Пирса) или И – ИЛИ - НЕ.

Дата добавления: 2013-12-13