КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение. По второму закону Ньютона уравнения
|
|
|
|
Решение
По второму закону Ньютона уравнения
движения грузов имеют вид:
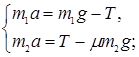
 , откуда
, откуда
 м/с2;
м/с2;
 Н.
Н.
Ответ: а =4,17 м/с2, Т =2,82 Н.
Задача 2. Снаряд массой 5 кг, вылетевший из орудия, в верхней точке траектории имеет скорость 300 м/с. В этой точке он разорвался на два осколка, причем больший осколок массой 3 кг полетел в обратном направлении со скоростью 100 м/с. Определить скорость второго, меньшего, осколка.
Дано: m =5 кг; v =300 м/с; m1 =3 кг; v1 =100 м/с.
Найти: v2.
По закону сохранения импульса 
 где
где 
 м/с.
м/с.
Ответ: v2 =900 м/с.
Задачи для самостоятельного решения
1. Тело массой 2 кг движется прямолинейно по закону  , где С =2 м/с2, D =0,4 м/с3. Определить силу, действующую на тело в конце первой секунды движения.
, где С =2 м/с2, D =0,4 м/с3. Определить силу, действующую на тело в конце первой секунды движения.
2. К нити подвешен груз массой 500 г. Определить силу натяжения нити, если нить с грузом: а) поднимать с ускорением 2 м/с2; б) опускать с тем же ускорением.
3. На тело массой 10 кг, лежащее на наклонной плоскости (угол α равен 200), действует горизонтально направленная сила 8 Н. Пренебрегая трением, определить: а) ускорение тела; б) силу, с которой тело давит на плоскость.
4. С вершины клина, длина которого 2 м и высота 1 м, начинает скользить небольшое тело. Коэффициент трения между телом и клином μ=0,15. Определить: а) ускорение, с которым движется тело; б) время прохождения тела вдоль клина; в) скорость тела у основания клина.
5. Два груза с неравными массами m1 и m2 (m1 > m2) подвешены на легкой нити, перекинутой через неподвижный блок. Считая нить и блок невесомыми и пренебрегая трением в оси блока, определить: а) ускорение грузов; б) силу натяжения нити.
6. Платформа с песком общей массой М =2 т стоит на рельсах на горизонтальном участке пути. В песок попадает снаряд массой m =8 кг и застревает в нем. Пренебрегая трением, определить, с какой скоростью будет двигаться платформа, если в момент попадания скорость снаряда 450 м/с, а ее направление – сверху вниз под углом 300 к горизонту.
7. На железнодорожной платформе, движущейся по инерции со скоростью 3 км/ч, укреплено орудие. Масса платформы с орудием 10 т. Ствол орудия направлен в сторону движения платформы. Снаряд массой 10 кг вылетает из ствола под углом 600 к горизонту. Определить скорость снаряда (относительно Земли), если после выстрела скорость платформы уменьшилась в 2 раза.
8. Человек массой 70 кг находится на корме лодки, длина которой 5 м и масса 280 кг. Человек переходит на нос лодки. На какое расстояние лодка передвинется по воде относительно дна?
9. Шарик массой 200 г ударился о стенку со скоростью 10 м/с и отскочил от нее с такой же скоростью. Определить импульс, полученный стенкой, если до удара шарик двигался под углом 300 к плоскости стенки.
10. Два шарика массами 2 и 4 кг двигаются со скоростями соответственно 5 и 7 м/с. Определить скорости шаров после прямого неупругого удара в случаях: а) больший шар догоняет меньший; б) шары двигаются навстречу друг другу.
ГЛАВА 3. РАБОТА И ЭНЕРГИЯ
3.1. Энергия, работа, мощность
Единая мера различных форм движения материи называется энергией. Энергия системы материальных тел характеризует эту систему с точки зрения возможных в ней количественных и качественных превращений движения. Эти превращения обусловлены как взаимодействием тел системы между собой, так и с внешними по отношению с системе телами.
Движение является неотъемлемым свойством материи. Поэтому всякое тело обладает энергией, являющейся мерой его движения. Для количественной характеристики качественно различных форм движения, изучаемых в физике, вводятся соответствующие им виды или формы энергии – механическая, внутренняя, электромагнитная и другие.
Причиной изменения состояния механического движения тела, а, следовательно, и его энергии, является взаимодействие тела с другими телами. Для характеристики воздействия этих тел на рассматриваемое тело в механике введено понятие силы. Поэтому можно говорить, что изменение движения и энергии вызывается силами. Процесс изменения энергии тела под действием силы называется процессом свершения работы, а приращение энергии тела в этом процессе называется работой, совершенной силой. Опыт показывает, что сила, приложенная к телу, совершает работу только тогда, если тело при этом перемещается.
 Из курса физики средней школы известно, что при прямолинейном поступательном движении тела работа, совершаемая постоянной силой
Из курса физики средней школы известно, что при прямолинейном поступательном движении тела работа, совершаемая постоянной силой  , тем больше, чем больше составляющая силы
, тем больше, чем больше составляющая силы 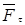 , касательная к траектории и чем больше путь s, пройденный телом за время действия силы:
, касательная к траектории и чем больше путь s, пройденный телом за время действия силы:
 (3.1)
(3.1)
В общем случае сила может изменяться как по величине, так и по направлению, поэтому формула (3.1) является лишь одним из частных случаев. Однако если рассматривать достаточно малое перемещение, то движение материальной точки можно считать прямолинейным, а силу – постоянной. Поэтому элементарная работа, совершаемая силой  на перемещении
на перемещении 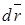 равна:
равна:
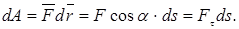 (3.1')
(3.1')
Работа, совершаемая силой  на конечном пути s (путь 1-2 на рис. 3.2), равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках:
на конечном пути s (путь 1-2 на рис. 3.2), равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках:
 (3.2)
(3.2)
Для вычисления этого интеграла надо знать зависимость 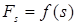 . Очевидно, что работа, совершаемая силой
. Очевидно, что работа, совершаемая силой  на пути 0-s, численно измеряется площадью, заштрихованной на рис. 3.3. Если сила
на пути 0-s, численно измеряется площадью, заштрихованной на рис. 3.3. Если сила 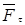 не зависит от s (
не зависит от s ( const), то
const), то 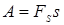 .
.
 Из выражения (3.1') следует, что сила, действующая на тело, не совершает работы, если:
Из выражения (3.1') следует, что сила, действующая на тело, не совершает работы, если:
а) тело покоится (ds =0);
б) сила перпендикулярна к направлению перемещения тела (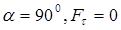 ).
).
Если угол  , то работа силы
, то работа силы 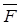 положительна (составляющая
положительна (составляющая  совпадает по направлению с вектором скорости
совпадает по направлению с вектором скорости  ), поэтому в данном случае силу
), поэтому в данном случае силу 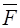 называют движущей силой. Если угол
называют движущей силой. Если угол 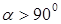 , то работа силы
, то работа силы  отрицательна (
отрицательна (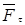 и
и  противоположны по направлению) и силу
противоположны по направлению) и силу  называют силой сопротивления (например, сила трения).
называют силой сопротивления (например, сила трения).
Единица работы – джоуль (Дж): 1 Дж – это работа, совершаемая силой в 1 Н на пути в 1 м:
1 Дж = 1 Н·м.
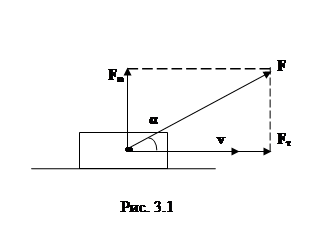
Если на тело, движущееся поступательно, одновременно действует несколько сил (рис. 3.4), то работа равнодействующей силы равна алгебраической сумме работ составляющих сил:


Если работа, совершаемая силой  при перемещении точки из одного произвольного положения 1 в другое произвольное положение 2 (рис. 3.5), не зависит от траектории перемещения, т.е. выполняется условие
при перемещении точки из одного произвольного положения 1 в другое произвольное положение 2 (рис. 3.5), не зависит от траектории перемещения, т.е. выполняется условие
А1-2 = А1-а-2 = А1-b-2,
то такая сила называется консервативной (или потенциальной).
Из уравнения (3.2) следует, что изменение направления движения вдоль траектории на противоположное вызывает изменение знака работы (cos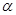 меняет свой знак). Поэтому при перемещении материальной точки вдоль замкнутой траектории L, например, 1-a-2-b-1, работа консервативной силы тождественно равна нулю:
меняет свой знак). Поэтому при перемещении материальной точки вдоль замкнутой траектории L, например, 1-a-2-b-1, работа консервативной силы тождественно равна нулю:

 (3.3)
(3.3)
Примерами консервативных сил являются силы всемирного тяготения, силы упругости, силы электростатического взаимодействия.
Все силы, не удовлетворяющие условию (3.3) (т.е. работа этих сил зависит от траектории перемещения точки), называются неконсервативными или диссипативными. Примером таких сил являются силы трения, которые всегда направлены в сторону, противоположную направлению движения ( ). Поэтому работа сил трения при перемещении материальной точки вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.
). Поэтому работа сил трения при перемещении материальной точки вдоль замкнутой траектории всегда отрицательна и никогда не равна нулю.
Для характеристики скорости совершения работы силой  , вводится понятие мощности, численно равной работе, совершаемой силой за единицу времени:
, вводится понятие мощности, численно равной работе, совершаемой силой за единицу времени:
 (3.4)
(3.4)
Подставляя в (3.4) выражение (3.1′) для элементарной работы, получим:
 (3.5)
(3.5)
Следовательно, мощность (мгновенная мощность) силы равна произведению касательной составляющей силы и скорости движения, т.е. скалярному произведению векторов силы и скорости. Если P ≠const, то пользуются понятием средней мощности за некоторый промежуток времени t, в течение которого сила совершила работу А:
 (3.6)
(3.6)
Единица мощности – ватт (Вт): 1 Вт – мощность, при которой за время 1 с совершается работа 1 Дж:
1 Вт = 1 Дж/с.
3.2. Виды механической энергии
В механике различают два вида энергии: кинетическую и потенциальную. Кинетической энергией называют механическую энергию всякого свободно движущегося тела и измеряют ее той работой, которую могло бы совершить тело при его торможении до полной остановки.
Пусть тело В, движущееся со скоростью  , начинает взаимодействовать с другим телом С и при этом тормозится. Следовательно, тело В действует на тело С с некоторой силой
, начинает взаимодействовать с другим телом С и при этом тормозится. Следовательно, тело В действует на тело С с некоторой силой  и на элементарном участке пути ds совершает работу
и на элементарном участке пути ds совершает работу
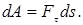
По третьему закону Ньютона на тело В одновременно действует сила  , касательная составляющая которой
, касательная составляющая которой  вызывает изменение численного значения скорости тела. Согласно второму закону Ньютона
вызывает изменение численного значения скорости тела. Согласно второму закону Ньютона
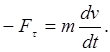
Следовательно,

Работа, совершаемая телом до полной его остановки равна:

Итак, кинетическая энергия поступательно движущегося тела равна половине произведения массы этого тела на квадрат его скорости:
 (3.7)
(3.7)
Из формулы (3.7) видно, что кинетическая энергия тела не может быть отрицательной ( ).
).
Если система состоит из n поступательно движущихся тел, то для ее остановки необходимо затормозить каждое из этих тел. Поэтому полная кинетическая энергия механической системы равна сумме кинетических энергий всех входящих в нее тел:
 (3.8)
(3.8)
Из формулы (3.8) видно, что Еk зависит только от величины масс и скоростей движения, входящих в нее тел. При этом неважно, каким образом тело массой mi приобрело скорость  . Другими словами, кинетическая энергия системы есть функция состояния ее движения.
. Другими словами, кинетическая энергия системы есть функция состояния ее движения.
Скорости  существенно зависят от выбора системы отсчета. При выводе формул (3.7) и (3.8) предполагалось, что движение рассматривается в инерциальной системе отсчета, т.к. иначе нельзя было бы использовать законы Ньютона. Однако, в разных инерциальных системах отсчета, движущихся относительно друг друга, скорость
существенно зависят от выбора системы отсчета. При выводе формул (3.7) и (3.8) предполагалось, что движение рассматривается в инерциальной системе отсчета, т.к. иначе нельзя было бы использовать законы Ньютона. Однако, в разных инерциальных системах отсчета, движущихся относительно друг друга, скорость  i -го тела системы, а, следовательно, его
i -го тела системы, а, следовательно, его  и кинетическая энергия всей системы будут неодинаковы. Таким образом, кинетическая энергия системы зависит от выбора системы отсчета, т.е. является величиной относительной.
и кинетическая энергия всей системы будут неодинаковы. Таким образом, кинетическая энергия системы зависит от выбора системы отсчета, т.е. является величиной относительной.
Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
Численно потенциальная энергия системы в данном ее положении равна работе, которую произведут действующие на систему силы при перемещении системы из этого положения в то, где потенциальная энергия условно принимается равной нулю (Еп = 0). Понятие «потенциальная энергия» имеет место только для консервативных систем, т.е. систем, у которых работа действующих сил зависит только от начального и конечного положения системы. Так, для груза весом P, поднятого на высоту h, потенциальная энергия будет равна  (Еп = 0 при h = 0); для груза, прикрепленного к пружине,
(Еп = 0 при h = 0); для груза, прикрепленного к пружине,  , где
, где 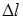 - удлинение (сжатие) пружины, k – ее коэффициент жесткости (Еп = 0 при l = 0); для двух частиц с массами m1 и m2, притягивающимися по закону всемирного тяготения,
- удлинение (сжатие) пружины, k – ее коэффициент жесткости (Еп = 0 при l = 0); для двух частиц с массами m1 и m2, притягивающимися по закону всемирного тяготения, 
 , где γ – гравитационная постоянная, r – расстояние между частицами (Еп = 0 при
, где γ – гравитационная постоянная, r – расстояние между частицами (Еп = 0 при  ).
).
Рассмотрим потенциальную энергию системы Земля – тело массой m, поднятого на высоту h над поверхностью Земли. Уменьшение потенциальной энергии такой системы измеряется работой сил тяготения, совершаемой при свободном падении тела на Землю. Если тело падает по вертикали, то

где Еno – потенциальная энергия системы при h = 0 (знак «-» показывает, что работа совершается за счет убыли потенциальной энергии).
Если это же тело падает по наклонной плоскости длиной l и с углом наклона 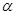 к вертикали (
к вертикали ( , то работа сил тяготения равна прежней величине:
, то работа сил тяготения равна прежней величине:

Если, наконец, тело движется по произвольной криволинейной траектории, то можно представить себе эту кривую состоящей из n малых прямолинейных участков 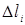 . Работа силы тяготения на каждом из таких участков равна
. Работа силы тяготения на каждом из таких участков равна
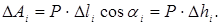
На всем криволинейном пути работа сил тяготения, очевидно, равна:

Итак, работа сил тяготения зависит только от разности высот начальной и конечной точек пути.
Таким образом, тело в потенциальном (консервативном) поле сил обладает потенциальной энергией. При бесконечно малом изменении конфигурации системы работа консервативных сил равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

В свою очередь работа dA выражается как скалярное произведение силы  на перемещение
на перемещение 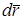 , поэтому последнее выражение можно записать следующим образом:
, поэтому последнее выражение можно записать следующим образом:
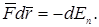 (3.9)
(3.9)
Следовательно, если известна функция Еп( r ), то из выражения (3.9) можно найти силу  по модулю и направлению.
по модулю и направлению.
Для консервативных сил
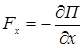 ,
,  ,
,  ,
,
или в векторном виде
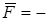 grad П,
grad П,
где
grad П  (3.10)
(3.10)
Вектор, определяемый выражением (3.10), называется градиентом скалярной функции П; 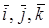 - единичные векторы координатных осей (орты).
- единичные векторы координатных осей (орты).
Конкретный вид функции П (в нашем случае Еп) зависит от характера силового поля (гравитационное, электростатическое и т.п.), что и было показано выше.
Полная механическая энергия W системы равна сумме ее кинетической и потенциальной энергий:

Из определения потенциальной энергии системы и рассмотренных примеров видно, что эта энергия, подобно кинетической энергии, является функцией состояния системы: она зависит только от конфигурации системы и ее положения по отношению к внешним телам. Следовательно, полная механическая энергия системы также является функцией состояния системы, т.е. зависит только от положения и скоростей всех тел системы.
3.3. Закон сохранения энергии в механике
Путь к правильному пониманию переходов движения из одной формы в другую был намечен М.В. Ломоносовым, который сформулировал закон сохранения массы вещества при химических превращениях и закон сохранения материи и движения. Количественную формулировку закона сохранения и превращения энергии дали немецкие ученые Ю. Майер и Г. Гельмгольц (XIX в.): в замкнутой системе энергия может переходить из одних видов в другие и передаваться от одного тела к другому, но ее общее количество остается неизменным.
Закон сохранения и превращения энергии является одним из фундаментальных законов природы, справедливым как для систем макроскопических тел, так и для систем элементарных частиц. Он является выражением вечности и неуничтожимости движения в природе, которое лишь переходит из одной формы в другую.
В замкнутой системе тел, силы взаимодействия между которыми консервативны (потенциальны), отсутствуют взаимные превращения механической энергии в другие виды энергии. Такие системы называются замкнутыми консервативными и для них справедлив закон сохранения энергии в механике: механическая энергия замкнутой консервативной системы не изменяется в процессе ее движения:
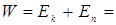 const. (3.11)
const. (3.11)
Для вывода этого закона рассмотрим систему материальных точек максами m1, m2, …, mn, движущихся со скоростями  . Пусть
. Пусть  - равнодействующие внутренних консервативных сил, действующие на каждую из этих точек, а
- равнодействующие внутренних консервативных сил, действующие на каждую из этих точек, а 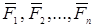 - равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действует еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим
- равнодействующие внешних сил, которые также будем считать консервативными. Кроме того, будем считать, что на материальные точки действует еще и внешние неконсервативные силы; равнодействующие этих сил, действующих на каждую из материальных точек, обозначим  При
При 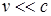 массы материальных точек постоянны и уравнения движения этих точек по второму закону Ньютона имеют следующий вид:
массы материальных точек постоянны и уравнения движения этих точек по второму закону Ньютона имеют следующий вид:
 (3.12)
(3.12)
Двигаясь под действием сил, точки системы за интервал времени dt совершают перемещения 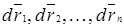 . Умножим каждое уравнение системы (3.12) на соответствующее перемещение:
. Умножим каждое уравнение системы (3.12) на соответствующее перемещение:

Учитывая, что  , получим:
, получим:

Складывая эти уравнения, получим:
 (3.13)
(3.13)
Первый член левой части (3.13) представляет собой приращение кинетической энергии системы:

Второй член  равен элементарной работе внутренних и внешних консервативных сил, т.е. равен элементарному приращению потенциальной энергии dEк.
равен элементарной работе внутренних и внешних консервативных сил, т.е. равен элементарному приращению потенциальной энергии dEк.
Правая часть уравнения (3.13) задает работу внешних неконсервативных сил, действующих на систему. Таким образом, имеем:
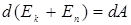 (3.14)
(3.14)
При переходе системы из состояния 1 в какое-либо состояние 2
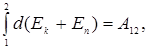
т.е изменение полной механической энергии системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (3.14) следует, что

откуда
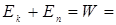 const,
const,
что и требовалось доказать.
Закон сохранения механической энергии связан с однородностью времени, т.е. инвариантностью физических законов относительно выбора начала отсчета времени.
Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние), называются консервативными системами. Системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие виды энергии, называются диссипативными (диссипация – рассеяние энергии). Строго говоря, все системы в природе являются диссипативными и в них закон сохранения механической энергии нарушается. Однако при изменении механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом состоит физическая сущность закона сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.
Во многих задачах рассматривается одномерное движение тела, потенциальная энергия которого является функцией лишь одной переменной (например, координаты х), т.е. Еп = f(х). График зависимости потенциальной энергии от некоторого аргумента называется потенциальной кривой, анализ которой позволяет определить характер движения тела.
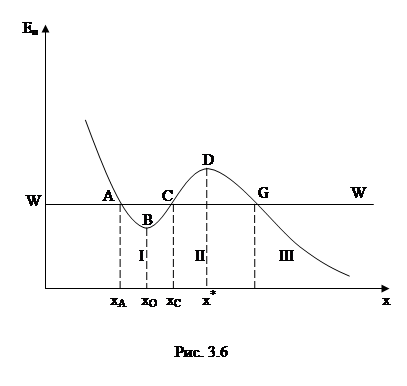 В общем случае потенциальная кривая может иметь достаточно сложный вид, например с несколькими максимумами и минимумами (рис. 3.6).
В общем случае потенциальная кривая может иметь достаточно сложный вид, например с несколькими максимумами и минимумами (рис. 3.6).
Проанализируем эту потенциальную кривую в предположении, что система консервативна и в ней выполняется закон сохранения энергии в форме (3.11). Если W - заданная полная энергия тела, то тело может находиться только там, где Еп(х) ≤ W, т.е. в областях I и III. Переходить из области I в область III и обратно тело не может, так как ему препятствует потенциальный барьер CDG, ширина которого равна интервалу значений х, при которых Еп > W, а его высота определяется разностью Епmax-W. Для того чтобы тело смогло преодолеть потенциальный барьер, ему необходимо сообщить дополнительную энергию, равную высоте барьера или превышающую ее. В области I тело с полной энергией W оказывается «запертым» в потенциальной яме ABC и совершает колебания между точками с координатами хА и хС.
В точке В с координатой хО потенциальная энергия тела минимальна. Так как действующая на тело сила 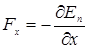 , а условие минимума потенциальной энергии
, а условие минимума потенциальной энергии 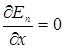 , то в точке В Fx =0. При смещении тела из положения хО в результате малых возмущений в системе оно испытывает действие возвращающей силы, поэтому положение хО является положением устойчивого равновесия. Указанные условия выполняются и для точки х* (для Епmax). Однако эта точка соответствует положению неустойчивого равновесия, так как при малых возмущениях в системе появляется сила, стремящаяся удалить тело от этого положения. Таким образом, в состоянии устойчивого равновесия замкнутой консервативной системы ее потенциальная энергия имеет минимальное значение, а в состоянии неустойчивого равновесия – максимальное значение.
, то в точке В Fx =0. При смещении тела из положения хО в результате малых возмущений в системе оно испытывает действие возвращающей силы, поэтому положение хО является положением устойчивого равновесия. Указанные условия выполняются и для точки х* (для Епmax). Однако эта точка соответствует положению неустойчивого равновесия, так как при малых возмущениях в системе появляется сила, стремящаяся удалить тело от этого положения. Таким образом, в состоянии устойчивого равновесия замкнутой консервативной системы ее потенциальная энергия имеет минимальное значение, а в состоянии неустойчивого равновесия – максимальное значение.
 Рассмотрим применение закона сохранения энергии в механике к расчету абсолютно упругого прямого центрального удара двух шаров. Абсолютно упругим называется такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии.
Рассмотрим применение закона сохранения энергии в механике к расчету абсолютно упругого прямого центрального удара двух шаров. Абсолютно упругим называется такой удар, в результате которого не происходит превращения механической энергии системы соударяющихся тел в другие виды энергии.
Пусть два абсолютно упругих шара массами m1 и m2 до удара движутся поступательно со скоростями 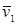 и
и 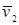 , направленными в одну сторону вдоль линии их центров, причем
, направленными в одну сторону вдоль линии их центров, причем 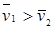 (рис. 3.7, а). Требуется найти скорости шаров
(рис. 3.7, а). Требуется найти скорости шаров  и
и  после их соударения (рис. 3.7, б).
после их соударения (рис. 3.7, б).
По закону сохранения энергии в механике имеем:
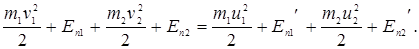 (3.15)
(3.15)
Шары движутся в горизонтальной плоскости, поэтому их потенциальная энергия в поле тяготения Земли при ударе не изменяется, т.е.
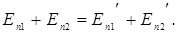
Тогда из уравнения (3.15) получаем:
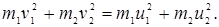 (3.16)
(3.16)
С другой стороны, по закону сохранения импульса
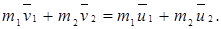 (3.17)
(3.17)
При центральном ударе векторы скоростей  ,
,  ,
,  и
и  направлены вдоль одной прямой. Поэтому в уравнении (3.17) можно перейти от векторов к их модулям:
направлены вдоль одной прямой. Поэтому в уравнении (3.17) можно перейти от векторов к их модулям:
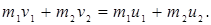 (3.18)
(3.18)
Решая совместно уравнения (3.16) и (3.18), получим:
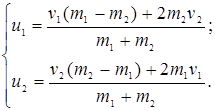 (3.19)
(3.19)
Анализ уравнений (3.19) позволяет сделать следующие выводы:
1) Если массы шаров одинаковы (m1=m2=m), то 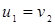 и
и  , т.е. при ударе шары обмениваются скоростями;
, т.е. при ударе шары обмениваются скоростями;
2) если масса второго шара m2>>m1, то
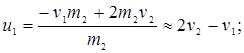

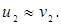
Если при этом второй шар был до удара неподвижен (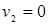 ), то
), то 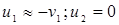 , т.е. первый шар отскакивает от неподвижного массивного шара и движется в обратную сторону со скоростью
, т.е. первый шар отскакивает от неподвижного массивного шара и движется в обратную сторону со скоростью  .
.
Как отмечалось, система тел называется диссипативной, если ее механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. В качестве примера рассмотрим диссипацию энергии при абсолютно неупругом прямом центральном ударе двух поступательно движущихся шаров (удар называется абсолютно неупругим, если после удара тела движутся как одно целое, т.е. с одной и той же скоростью).
Общая скорость обоих шаров после удара по закону сохранения импульса равна:
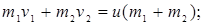
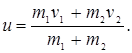 (3.20)
(3.20)
Если шары движутся в горизонтальной плоскости, то их потенциальная энергия Еn остается неизменной. Полная механическая энергия системы до удара

После удара она будет равна
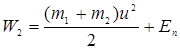 , или, с учетом (3.20):
, или, с учетом (3.20):

Найдем изменение полной механической энергии системы в результате неупругого удара:

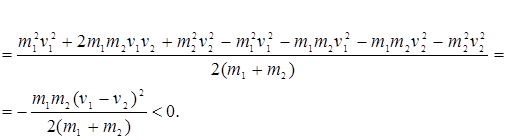
Таким образом, при неупругом ударе полная механическая энергия системы уменьшается, т.е. часть ее рассеивается на деформацию соударяющихся тел. На деформацию тел затрачивается работа, равная убыли полной механической энергии системы:

Если второе тело до удара было неподвижно (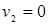 ), то
), то
 (3.21)
(3.21)
Неупругий удар на практике применяется для целей двоякого рода. Во-первых, для изменения формы тела – ковки и штамповки металла, раздробления тел. В этом случае важно, чтобы возможно большая часть кинетической энергии первого тела затрачивалась на работу деформации (формула (3.21)), т.е. чтобы масса неподвижного тела m2 (например, наковальни вместе с куском металла) была во много раз больше массы ударяющего тела m1 (например, молота).
Вторая цель состоит в перемещении тел после удара и преодолении при этом сопротивлений (забивка свай в землю, вбивание клиньев и т.п.). В этом случае выгодно, чтобы работа, затрачиваемая на деформацию, была как можно меньше и чтобы общая кинетическая энергия обоих тел после удара ( ) была наибольшей. Для этого необходимо, чтобы масса ударяющего тела m1 (молота) была во много раз больше массы второго тела m2 (сваи, гвоздя).
) была наибольшей. Для этого необходимо, чтобы масса ударяющего тела m1 (молота) была во много раз больше массы второго тела m2 (сваи, гвоздя).
Краткие выводы
· Энергия – универсальная мера различных форм движения материальных объектов и их взаимодействия. Количественной характеристикой процесса обмена энергией между взаимодействующими телами является физическая скалярная величина – работа сил.
Элементарная работа силы
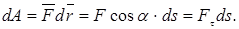
Работа силы на произвольном участке траектории 1-2

· Мощность – физическая скалярная величина, характеризующая скорость совершения работы:

Мощность, развиваемая силой  в данный момент времени, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы:
в данный момент времени, равна скалярному произведению вектора силы на вектор скорости, с которой движется точка приложения этой силы:

· Консервативная сила – сила, работа которой при перемещении из одного положения в другое не зависит от траектории перемещения, а зависит только от начального и конечного положений тела. Силовое поле, в котором консервативные силы совершают работу, называется потенциальным полем.
· Кинетическая энергия - механическая энергия всякого свободно движущегося тела, численно равная работе, которую совершают действующие на тело силы при его торможении до полной остановки:

· Потенциальная энергия – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.
· Связь между консервативной силой  и потенциальной энергией устанавливается выражением
и потенциальной энергией устанавливается выражением
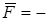 grad Еп,
grad Еп,
где
grad Еп = 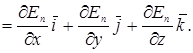
Отсюда, как частные случаи, определяются: а) потенциальная энергия тела массой m на высоте h
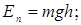
б) потенциальная энергия упругодеформированного тела

где k – коэффициент упругости (для пружины – жесткость).
· Полная энергия механической системы – равна сумме кинетической и потенциальной энергий:

· Механические системы, на тела которых действуют только консервативные силы (внутренние и внешние) называются консервативными системами. В таких системах выполняется закон сохранения механической энергии:
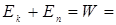 const,
const,
т.е. полная механическая энергия консервативной системы со временем не изменяется. Это фундаментальный закон природы, ко торый является следствием однородности времени.
· Система, в которой механическая энергия постепенно уменьшается за счет преобразования в другие формы энергии, называется диссипативной. Строго говоря, все системы в природе являются диссипативными. Однако при уменьшении механической энергии всегда возникает эквивалентное количество энергии другого вида. Другими словами, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом заключается физическая сущность всеобщего закона сохранения и превращения энергии – неуничтожимость материи и ее движения.
Вопросы для самоконтроля и повторения
1. Что такое энергия, работа, мощность?
2. Как определяется работа переменной силы?
3. Какие силы называются консервативными? Приведите примеры консервативных сил.
4. Какие силы называются диссипативными? Приведите примеры таких сил.
5. Дайте определения кинетической и потенциальной энергии.
6. В чем заключается закон сохранения механической энергии? Для каких систем он выполняется?
7. Каким свойством времени обусловлена справедливость закона сохранения механической энергии?
8. В чем физическая сущность закона сохранения и превращения энергии? Почему он является фундаментальным законом природы?
9. Как на основе закона сохранения механической энергии охарактеризовать положения устойчивого и неустойчивого равновесия консервативной системы?
10. Что такое потенциальная яма? потенциальный барьер?
Примеры решения задач
Задача 1. С башни высотой 20 м горизонтально со скоростью 10 м/с брошен камень массой 400 г (рис. 3.8). Пренебрегая сопротивлением воздуха, определить кинетическую и потенциальную энергию камня через 1 с после начала движения.
Дано: H = 20 м; v0 = 10 м/с; m = 0,4 кг; t = 1c.
Найти: Ek, Eп.
 Решение
Решение
В точке А 
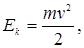
 где
где 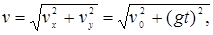
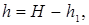
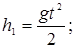


Подставляя числовые данные, получим Ek = 39,2 Дж, Eп = 59,2 Дж.
Ответ: Ek = 39,2 Дж, Eп = 59,2 Дж.
 Задача 2. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути (рис. 3.9). Определить: а) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1; б) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.
Задача 2. Автомобиль массой 1,8 т движется в гору, уклон которой составляет 3 м на каждые 100 м пути (рис. 3.9). Определить: а) работу, совершаемую двигателем автомобиля на пути 5 км, если коэффициент трения равен 0,1; б) развиваемую двигателем мощность, если известно, что этот путь был преодолен за 5 мин.
Дано: m = 1800 кг; sinα = 0,03; s = 5000 м; μ = 0,1; t = 300 с.
Найти: А, Р.
Решение

 где
где 
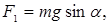

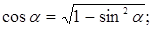
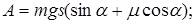

Подставляя числовые данные, получим:
А = 11,5·106 Дж, Р = 38,3·103 Вт.
Ответ: А = 11,5 МДж, Р = 38,3·кВт.
Задачи для самостоятельного решения
1. Тело массой 5 кг поднимают с ускорением 2 м/с2. Определить работу силы в течение первых пяти секунд.
2. Определить работу, совершаемую при подъеме груза массой 50 кг по наклонной плоскости с углом наклона 300 к горизонту на расстояние 4 м, если время подъема составляет 2 с, а коэффициент трения 0,06.
3. С башни высотой 35 м горизонтально брошен камень массой 0,3 кг. Пренебрегая сопротивлением воздуха, определить: а) скорость, с которой брошен камень, если через 1 с после начала движения его кинетическая энергия равна 60 Дж; б) потенциальную энергию камня через 1 с после начала движения.
4. Пуля массой 10 г, летевшая горизонтально со скоростью 500 м/с, попадает в баллистический маятник длиной 1 м и массой 5 кг и застревает в нем. Определить угол отклонения маятника.
5. Тело скользит с наклонной плоскости высотой h и углом наклона α к горизонту и движется далее по горизонтальному участку. Принимая коэффициент трения на всем пути постоянным и равным µ, определить расстояние s, пройденное телом на горизонтальном участке, до полной остановки.
6. Автомобиль массой 1,8 т спускается при выключенном двигателе с постоянной скоростью 54 км/ч по наклонной плоскости (угол к горизонту 30). Определить, какой должна быть мощность двигателя автомобиля, чтобы он смог подняться на такой же подъем с той же скоростью.
7. Камень массой 0,2 кг бросили под углом 600 к горизонту со скоростью 15 м/с. Найти кинетическую, потенциальную и полную энергию камня: а) спустя 1 с после начала движения; б) в высшей точке траектории. Сопротивлением воздуха пренебречь.
8. Тело массой 5 кг падает с высоты 20 м. Определить полную энергию тела в точке, находящейся от поверхности Земли на высоте 5 м. Трением тела о воздух пренебречь. Сравнить эту энергию с первоначальной энергией тела.
9. Тело, падая с некоторой высоты, в момент соприкосновения с Землей обладает импульсом 100 кг·м/с и кинетической энергией 500 Дж. Определить: а) с какой высоты тело падало; б) массу тела.
10. Тело брошено под углом 450 к горизонту со скоростью v0 =15 м/с. Используя закон сохранения энергии, определить скорость тела в высшей точке его траектории.
ГЛАВА 4. ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ТВЕРДОГО ТЕЛА
4.1. Характеристики динамики вращательного движения
Всякое твердое тело можно рассматривать как систему из n материальных точек и масса m тела есть сумма масс всех этих точек:
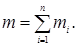
Будем считать, что тело абсолютно твердое, т.е. расстояния между любыми двумя его материальными точками не изменяются в процессе движения.
Рассмотрим движение твердого тела, закрепленного о одной неподвижной точке О, вокруг которой тело может свободно вращаться. Эта точка называется центром вращения тела. Совместим с этой точкой начало неподвижной системы координат. Тогда положение в пространстве i -точки тела определяется радиусом-вектором 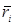 , проведенным из центра О в эту точку (рис. 4.1).
, проведенным из центра О в эту точку (рис. 4.1).
 Обозначим через
Обозначим через 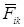 силу, действующую на i -ю точку тела со стороны k -ой его точки, и через
силу, действующую на i -ю точку тела со стороны k -ой его точки, и через  – равнодействующую всех внешних сил, приложенных к i -й точке. По второму закону Ньютона уравнение движения этой материальной точки имеет следующий вид:
– равнодействующую всех внешних сил, приложенных к i -й точке. По второму закону Ньютона уравнение движения этой материальной точки имеет следующий вид:


(k≠i, т.к. i -я точка сама на себя не действует).
Умножим обе части этого уравнения векторно на 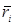 :
:
 (4.1)
(4.1)
Векторное произведение радиуса-вектора 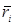 материальной точки на ее импульс
материальной точки на ее импульс 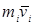 называется моментом импульса
называется моментом импульса  этой материальной точки относительно точки О:
этой материальной точки относительно точки О:
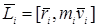 . (4.2)
. (4.2)
Вектор  называют также моментом количества движения материальной точки. Он направлен перпендикулярно к плоскости, проведенной через векторы
называют также моментом количества движения материальной точки. Он направлен перпендикулярно к плоскости, проведенной через векторы 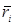 и
и 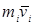 , и образует с ними правую тройку векторов: при наблюдении из конца
, и образует с ними правую тройку векторов: при наблюдении из конца  видно, что вращение от
видно, что вращение от 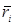 к
к 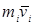 по кратчайшему расстоянию происходит против часовой стрелки.
по кратчайшему расстоянию происходит против часовой стрелки.
Векторное произведение радиуса-вектора 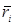 , проведенного из центра О в точку приложения внешней силы
, проведенного из центра О в точку приложения внешней силы  (рис. 4.2), на эту силу, называется моментом
(рис. 4.2), на эту силу, называется моментом  силы
силы  относительно точки О:
относительно точки О:
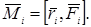 (4.3)
(4.3)
 Векторы
Векторы 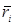 ,
,  и
и  также образуют правую тройку. Модуль момента силы, как следует из рисунка, равен:
также образуют правую тройку. Модуль момента силы, как следует из рисунка, равен:


где li – плечо силы  , т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.
, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы.
Моментом инерции тела относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек тела на квадраты их расстояний до рассматриваемой оси:
 (4.4)
(4.4)
В случае непрерывного распределения масс эта сумма сводится к интегралу
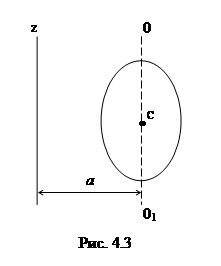
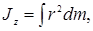
где интегрирование производится по всему объему тела. Величина r в данном случае есть функция положения точки с координатами x, y, z.
Неподвижная ось вращения z может проходить как через центр инерции тела (ось вращения маховика, ротора турбины и т.п.), так и вне его (например, ось вращения самолета, выполняющего мертвую петлю). Если известен момент инерции тела относительно оси, проходящей через его центр масс (инерции), то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера (теоремой о переносе осей инерции): момент инерции тела J z относительно произвольной оси вращения z равен сумме момента инерции тела относительно оси ОО1, проведенной через центр инерции С тела параллельно оси z и произведения массы тела на квадрат расстояния между этими осями (рис. 4.3):
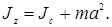 (4.5)
(4.5)
Таким образом, с удалением центра инерции тела от его оси вращения момент инерции тела относительно этой оси возрастает. Из формул (4.4) и (4.5) видно, что момент инерции тела зависит не только от его массы, но и от ее распределения относительно оси вращения.
В табл. 4.1 приведены значения моментов инерции для некоторых однородных тел.
Таблица 4.1
| Тело | Положение оси вращения | Момент инерции |
| Полый тонкостенный цилиндр радиуса R | Ось симметрии | 
|
| Сплошной цилиндр или диск радиуса R | То же | 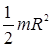
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | 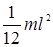
|
| Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | 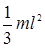
|
| Шар радиусом R | Ось проходит через центр шара | 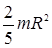
|
4.2. Уравнение динамики вращательного движения твердого тела
Выведем уравнение динамики вращательного движения тела. Из выражений (4.1), (4.2) и (4.3) следует, что скорость изменения момента импульса i -й материальной точки определяется следующим образом:
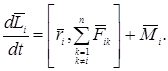 (4.6)
(4.6)
Сложим почленно уравнения (4.6), записанные для каждой из материальных точек тела:
 (4.7)
(4.7)
Векторная сумма моментов  всех внешних сил, приложенных к телу, называется результирующим, или главным, моментом
всех внешних сил, приложенных к телу, называется результирующим, или главным, моментом 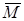 внешних сил относительно точки О:
внешних сил относительно точки О:

Векторная сумма моментов импульса  всех материальных точек тела называется моментом импульса
всех материальных точек тела называется моментом импульса  тела относительно точки О:
тела относительно точки О:
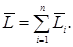
Так как производная от суммы равна сумме производных от всех слагаемых, то

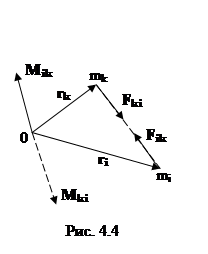 Наконец, векторная сумма моментов относительно точки О всех внутренних сил
Наконец, векторная сумма моментов относительно точки О всех внутренних сил 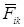 взаимодействия между точками тела равна нулю, т.е.
взаимодействия между точками тела равна нулю, т.е.
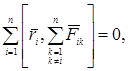
так как по третьему закону Ньютона силы 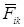 и
и  численно равны, имеют общую линию действия, но направлены в противоположные стороны (рис. 4.4). Поэтому их моменты
численно равны, имеют общую линию действия, но направлены в противоположные стороны (рис. 4.4). Поэтому их моменты  и
и  относительно точки О численно равны и противоположны по направлению (на рис. 4.4 точки mi, mk и О лежат в горизонтальной плоскости, а векторы
относительно точки О численно равны и противоположны по направлению (на рис. 4.4 точки mi, mk и О лежат в горизонтальной плоскости, а векторы  и
и 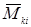 перпендикулярны этой плоскости). Действительно,
перпендикулярны этой плоскости). Действительно,  , где
, где 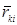 - вектор, проведенный из точки mi в точку mk. Поэтому
- вектор, проведенный из точки mi в точку mk. Поэтому  так как векторное произведение векторов
так как векторное произведение векторов 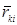 и
и  , направленных вдоль одной прямой, равно нулю.
, направленных вдоль одной прямой, равно нулю.
На основании изложенного уравнение (4.7) можно записать в следующем виде:

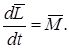 (4.8)
(4.8)
Таким образом, скорость изменения момента импульса тела, вращающегося вокруг неподвижной точки, равна результирующему моменту относительно этой точки всех внешних сил, приложенных к телу.
Полученный результат называется основным законом динамики вращательного движения тела, закрепленного в одной неподвижной точке. Момент импульса является основной динамической характеристикой твердого тела, вращающегося вокруг неподвижной точки.
4.3. Кинетическая энергия и работа при вращении тела
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси. Если мысленно разбить это тело на n точек массами m1, m2, …, mn, находящихся на расстояниях r1, r2, …, rn от оси вращения, то при вращении они будут описывать окружности и двигаться с различными линейными скоростями v1, v2, …, vn. Так как тело абсолютно твердое, то угловая скорость вращения точек будет одинакова:
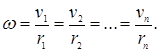
Кинетическая энергия вращающегося тела есть сумма кинетических энергий его точек, т.е.
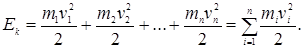
Учитывая связь между угловой и линейной скоростями, получим:
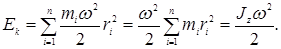 (4.9)
(4.9)
Сопоставление формулы (4.9) с выражением для кинетической энергии тела, движущегося поступательно со скоростью v, показывает, что момент инерции является мерой инертности тела во вращательном движении.
Если твердое тело движется поступательно со скоростью v и одновременно вращается с угловой скоростью ω вокруг оси, проходящей через его центр инерции, то его кинетическая энергия определяется как сумма двух составляющих:
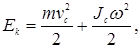 (4.10)
(4.10)
 где vc – скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс.
где vc – скорость центра масс тела; Jc - момент инерции тела относительно оси, проходящей через его центр масс.
Моментом силы относительно неподвижной оси z называется скалярная величина Mz, равная проекции на эту ось вектора 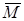 момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента Mz не зависит от выбора положения точки 0 на оси z.
момента силы, определенного относительно произвольной точки 0 данной оси. Значение момента Mz не зависит от выбора положения точки 0 на оси z.
Если ось z совпадает с направлением вектора 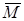 , то момент силы представляется в виде вектора, совпадающего с осью:
, то момент силы представляется в виде вектора, совпадающего с осью:

Найдем выражение для работы при вращении тела. Пусть сила  приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором
приложена к точке В, находящейся от оси вращения на расстоянии r (рис. 4.6); α – угол между направлением силы и радиусом-вектором  . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.
. Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела.
 При повороте тела на бесконечно малый угол
При повороте тела на бесконечно малый угол 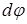 точка приложения В проходит путь
точка приложения В проходит путь 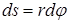 , и работа равна произведению проекции силы на направление смещения на величину смещения:
, и работа равна произведению проекции силы на направление смещения на величину смещения:
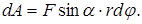
Учитывая, что  можно записать
можно записать 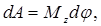 где Mz - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
где Mz - момент силы относительно оси вращения. Таким образом, работа при вращении тела равна произведению момента действующей силы на угол поворота.
Работа при вращении тела идет на увеличение его кинетической энергии:

где 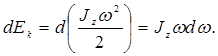 Тогда
Тогда  , или
, или  Учитывая, что
Учитывая, что  получим
получим
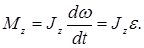 (4.11)
(4.11)
Уравнение (4.11) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.
4.4. Закон сохранения момента импульса
Моментом импульса относительно неподвижной оси z называется скалярная величина Lz, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки 0 данной оси. Значение момента импульса Lz не зависит от положения точки 0 на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси каждая отдельная точка тела движется по окружности постоянного радиуса  с некоторой скоростью
с некоторой скоростью 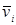 . Скорость
. Скорость