Решение. Согласно уравнению динамики вращательного движения твердого тела относительно неподвижной оси

Решение

Согласно уравнению динамики вращательного движения твердого тела относительно неподвижной оси

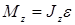, где - момент инерции шара;

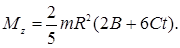
Для t =3 c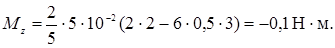

Ответ: M_z =-0,1 Н·м.

Задача 2. На однородный сплошной цилиндрический вал радиусом 20 см, момент инерции которого 0,15 кг·м², намотана легкая нить, к концу которой прикреплен груз массой 0,5 кг. До начала вращения барабана высота груза над полом составляла 2,3 м (рис.). Определить: а) время опускания груза до пола; б) силу натяжения нити; в) кинетическую энергию груза в момент удара о пол.

Дано: R =0,2 м; J_z =0,15 кг·м²; m =0,5 кг; h =2,3 м.

Найти: t, T, E_к.

По закону сохранения энергии

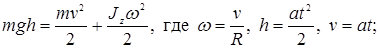
откуда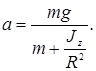

Время опускания груза до пола:

.

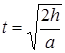Уравнение динамики вращательного движения вала 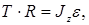откуда сила натяжения нити

тогда .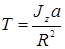

Кинетическая энергия груза в момент удара о пол:

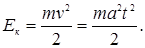
Ответ: t =2 с; Т =4,31 Н; Е_к =1,32 Дж.

Задачи для самостоятельного решения

1. Шар и сплошной цилиндр, изготовленные из одного и того же материала, одинаковой массы катятся без скольжения с одинаковой скоростью. Определить, во сколько раз кинетическая энергия шара меньше кинетической энергии сплошного цилиндра.

2. Полый тонкостенный цилиндр массой 0,5 кг, катящийся без скольжения, ударяется о стену и откатывается от нее. Скорость цилиндра до удара о стену 1,4 м/с, после удара 1 м/с. Определить выделившееся при ударе количество теплоты.

3. К ободу однородного сплошного диска массой 10 кг, насаженного на ось, приложена постоянная касательная сила 30 Н. Определить кинетическую энергию через 4 с после начала действия силы.

4. Вентилятор вращается с частотой 600 об/мин. После выключения он начал вращаться равнозамедленно и, сделав 50 оборотов, остановился. Работа сил торможения равна 31,4 Дж. Определить: а) момент сил торможения; б) момент инерции вентилятора.

5. К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения 2 Н·м. Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с².

6. С наклонной плоскости, составляющей угол 30⁰ с горизонтом, скатывается без скольжения шарик. Пренебрегая трением, определить время движения шарика по наклонной плоскости, если известно, что его центр масс при скатывании понизился на 30 см.

7. На однородный сплошной цилиндрический вал радиусом 50 см намотана легкая нить, к концу которой прикреплен груз массой 6,4 кг. Груз, разматывая нить, опускается с ускорением 2 м/с². Определить: а) момент инерции вала; б) массу вала.

8. Горизонтальная платформа массой 25 кг и радиусом 0,8 м вращается с частотой 18 об/мин. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, определить частоту вращения платформы, если человек, опустив руки, уменьшит свой момент инерции от 3,5 кг·м² до 1 кг·м².

9. Человек массой 60 кг, стоящий на краю горизонтальной платформы массой 120 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 об/мин, переходит к ее центру. Считая платформу круглым однородным диском, а человека – точечной массой, определить, с какой частотой будет тогда вращаться платформа.

10. Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Определить, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

ГЛАВА 5. ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ

ОТНОСИТЕЛЬНОСТИ

5.1. Механический принцип относительности

и законы электродинамики

Во второй половине XIX века Д. Максвеллом были сформулированы основные законы электродинамики. При этом возникли сомнения в справедливости механического принципа относительности Галилея применительно к электромагнитным явлениям. Вспомним суть механического принципа относительности.

Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны); в этом состоит суть механического принципа относительности или принципа относительности Галилея.

Для доказательства этого принципа рассмотрим две системы отсчета: инерциальную систему К (с координатами x, y, z), которую условно будем считать неподвижной и подвижную систему 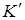(с координатами ), движущуюся относительно К равномерно и прямолинейно со скоростью = const. Примем, что в начальный момент времени t = 0 начала О и 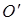обеих систем координат совпадают. Расположение систем координат в произвольный момент времени t имеет вид, изображенный на рис. 5.1. Скорость направлена вдоль прямой , а радиус-вектор, проведенный из точки О в точку 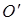, равен

Координаты произвольной материальной точки А в неподвижной и подвижной системах отсчета определяются радиусами-векторами и 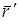, причем

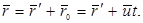(5.1)

В проекциях на оси координат векторное уравнение (5.1) записывается в виде, называемом преобразованиями Галилея:

(5.2)

В частном случае, когда система 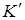движется со скоростью вдоль положительного направления оси х системы К, преобразования координат Галилея имеют следующий вид:

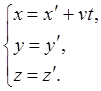
В классической механике предполагается, что ход времени не зависит от относительного движения систем отсчета. Поэтому система уравнений (5.2) дополняется еще одним соотношением:

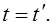(5.3)

Соотношения (5.2) – (5.3) справедливы лишь в случае . При скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца.

Продифференцируем уравнение (5.1) по времени и учитывая, что =const, найдем соотношения между скоростями и ускорениями точки А относительно обеих систем отсчета:

откуда

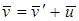, (5.4)

а также

(5.5)

Если на точку А другие тела не действуют, то 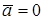и согласно (5.5) 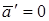, т.е. подвижная система К΄ является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.

Из выражения (5.5) следует, что

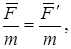или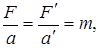

т.е. уравнения Ньютона (уравнения динамики) для материальной точки одинаковы во всех инерциальных системах отсчета или инвариантны по отношению к преобразованиям Галилея. Этот результат часто формулируют следующим образом: равномерное и прямолинейное движение системы как целого не влияет на ход протекающих в ней механических процессов.

Классическая механика Ньютона достоверно описывает движение макроскопических тел, движущихся со скоростями, намного меньшими скорости света. В конце XIX в. было установлено, что выводы классической механики противоречат некоторым опытным данным. В частности при изучении движения быстрых заряженных частиц оказалось, что их движение не подчиняется законам Ньютона. Далее возникли затруднения при попытках применить классическую механику для объяснения распространения света. Согласно законам электродинамики скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям и приблизительно равна с = 3·10⁸ м/с. Но в соответствии с законами классической физики скорость света может равняться с только в одной избранной системе отсчета. В любой другой системе отсчета, движущейся относительно избранной системы со скоростью v, она должна уже равняться c-v, или c+v. Это означает, что если справедлив закон сложения скоростей классической механики (формула (5.4)), то при переходе от одной инерциальной системы к другой законы электродинамики должны меняться, так как должна меняться скорость света. Таким образом, обнаружились противоречия между электродинамикой и механикой Ньютона, законы которой согласуются с принципом относительности Галилея. Для преодоления возникших трудностей предлагались различные способы:

1. Принять несостоятельность принципа относительности применительно к электромагнитным явлениям. Еще со времен Фарадея электромагнитные явления рассматривались как процессы в особой, всепроникающей среде, заполняющей все пространство, - эфире. Согласно Х. Лоренцу инерциальная система отсчета, покоящаяся относительно эфира, - это особая система, в которой законы электродинамики Максвелла справедливы. Лишь в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.

2. Считать ошибочными уравнения электродинамики Максвелла и попытаться изменить их таким образом, чтобы они при переходе от одной инерциальной системы к другой (в соответствии с классическими представлениями о пространстве и времени) не менялись. Такая попытка, в частности, была предпринята Г. Герцем, который считал, что эфир полностью увлекается движущимися телами, поэтому электромагнитные явления протекают одинаково, независимо от того, покоится тело или движется. Принцип относительности справедлив.

3. Отказаться от классических представлений о пространстве и времени, с тем, чтобы сохранить и принцип относительности, и законы Максвелла. С этой точки зрения оказываются неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени. Таким образом, изменять нужно законы классической механики, а не законы электродинамики Максвелла.

Вспомним, как трактовались пространство и время в классической физике. Пространство рассматривалось как бесконечная пустая протяженность, вмещающая в себе все тела и не зависящая от материи. Время рассматривалось как абсолютный фактор равномерного потока длительности, в котором все возникает и исчезает. При этом время не зависит ни от каких процессов в мире.

Развитие естествознания опровергло эти представления. Никакого абсолютного пространства и времени не существует. Вселенная заполнена материей в форме вещества и поля, а пространство выступает как всеобщее свойство материи. Время всегда связано с движением и развитием материи. Таким образом, пространство – это форма бытия материи, которая выражает ее протяженность и структурность; время – это форма бытия материи, характеризующая длительность существования всех объектов, полей и последовательность смены событий.

Основными свойствами пространства и времени являются: а) единство и неразрывная связь материи, пространства и времени; б) абсолютная непрерывность и относительная прерывность пространства и времени. Непрерывность проявляется в распространении материальных полей в пространстве всех тел и систем, в бесконечном следовании элементов длины при движении тела между двумя точками. Прерывность пространства относительна и проявляется в раздельном существовании материальных объектов и систем, каждая из которых имеет определенные размеры и границы. Прерывность времени характеризуется лишь временем существования качественных состояний материи, каждое из которых возникает и исчезает, переходя в другие формы; в) время обладает длительностью, однонаправленностью, необратимостью.

Последовательно развивая новые, отличные от классических, представления о пространстве и времени, А. Эйнштейн в начале XX в. создал специальную теорию относительности (СТО). В рамках этой теории удалось согласовать принцип относительности с электродинамикой Максвелла. При этом новая теория не отменяла старую (ньютоновскую механику), а включала ее в себя как частный, предельный случай.

5.2. Постулаты специальной теории относительности.

Преобразования Лоренца

Специальная теория относительности представляет собой современную физическую теорию пространства и времени. В СТО, как и в классической механике, предполагается, что время однородно (инвариантность физических законов относительно выбора начала отсчета времени), а пространство однородно и изотропно (симметрично). Специальная теория относительности называется также релятивистской теорией, а явления, описываемые этой теорией – релятивистскими эффектами.

В основу СТО легло положение, согласно которому никакая энергия, никакой сигнал не могут распространяться со скоростью, превышающей скорость света в вакууме, а скорость света в вакууме постоянна и не зависит от направления распространения.

Это положение формулируется в виде двух постулатов А. Эйнштейна: принципа относительности и принципа постоянства скорости света.

Первый постулат является обобщением механического принципа относительности Галилея на любые физические процессы и утверждает, что законы физики имеют одинаковую форму (инвариантны) во всех инерциальных системах отсчета: любой процесс протекает одинаково в изолированной материальной системе, находящейся в состоянии покоя, и в такой же системе, находящейся в состоянии равномерного прямолинейного движения. Состояние покоя или движения определяется здесь относительно произвольно выбранной инерциальной системы отсчета; физически эти состояния равноправны.

Второй постулат утверждает: скорость света в вакууме не зависит от скорости движения источника света или наблюдателя и одинакова во всех инерциальных системах отсчета.

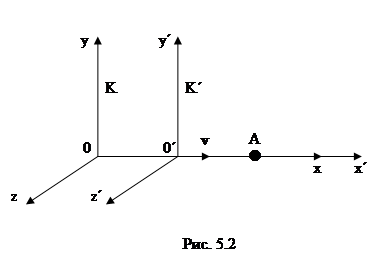Анализ явлений в инерциальных системах отсчета, проведенный А. Эйнштейном на базе сформулированных им постулатов, показал, что преобразования Галилея несовместимы с ними и, следовательно, должны быть заменены преобразованиями, удовлетворяющими постулатам СТО.

Рассмотрим две инерциальные системы отсчета: К (с координатами x, y, z) и К ΄ (с координатами x΄, y΄, z΄), движущуюся относительно К вдоль оси х со скоростью =const. Пусть в начальный момент времени (t = t΄ = 0), когда начала систем координат совпадают (0 = 0΄), излучается световой импульс. Согласно второму постулату Эйнштейна скорость света в обеих системах одна и та же и равна с. Поэтому если за время t в системе К сигнал дойдет до некоторой точки А, пройдя расстояние

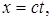(5.6)

то в системе К΄ координата светового импульса в момент достижения точки А будет равна

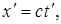(5.7)

где t΄ - время прохождения светового импульса от начала координат до точки А в системе К΄. Вычитая (5.6) из (5.7), получим:

Так как 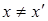(система К΄ перемещается относительно К), то получается, что , т.е. отсчет времени в системах К΄ и К различен или имеет относительный характер (в классической механике считается, что время во всех инерциальных системах отсчета протекает одинаково, т.е. t = t΄).

А. Эйнштейн показал, что в СТО классические преобразования Галилея при переходе от одной инерциальной системы отсчета к другой заменяются преобразованиями Лоренца (1904 г.), удовлетворяющими первому и второму постулатам (табл. 5.1).

Таблица 5.1

Прямые	преобразования	Обратные	преобразования
Галилея	Лоренца	Галилея	Лоренца

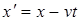
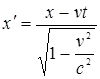
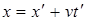
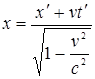
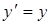
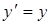
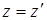
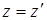
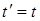
Из преобразований Лоренца вытекает, что при малых скоростях (по сравнению со скоростью света) они переходят в преобразования Галилея. При v>c выражения для x, t, x΄ и t΄ теряют физический смысл, т.е. движение со скоростью, большей скорости света в вакууме, невозможно. Кроме того, из табл. 5.1 следует, что как пространственные, так и временные преобразования Лоренца не являются независимыми: в закон преобразования координат входит время, а в закон преобразования времени - пространственные координаты, т.е. устанавливается взаимосвязь пространства и времени. Таким образом, релятивистская теория Эйнштейна оперирует не трехмерным пространством, к которому присоединяется понятие времени, а рассматривает неразрывно связанные пространственные и временные координаты, образующие четырехмерное пространство-время.

5.3. Следствия из преобразований Лоренца

1. Относительность одновременности. Пусть в системе К в точках с координатами х₁ и х₂ в моменты времени t₁ и t₂ происходят два события. В системе К΄ им соответствуют координаты 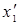и 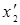и моменты времени и 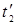. Если события в системе К происходят в одной точке (х₁=х₂) и являются одновременными (t₁=t₂), то, согласно преобразованиям Лоренца,

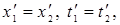
т.е. эти события являются одновременными и пространственно совпадающими для любой инерциальной системы отсчета.

Если события в системе К пространственно разобщены (х₁ ≠ х₂), но одновременны (t₁=t₂), то в системе К΄, согласно преобразованиям Лоренца,

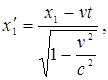
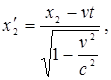
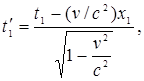
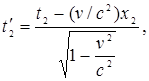
Таким образом, в системе К΄ эти события, оставаясь пространственно разобщенными, оказываются и неодновременными.

2. Длительность событий в разных системах отсчета. Пусть в некоторой точке А с координатой х, покоящейся относительно системы К, происходит событие, длительность которого (разность показаний часов в конце и начале события) , где индексы 1 и 2 соответствуют началу и концу события. Длительность этого же события в системе К΄

,

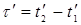где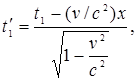

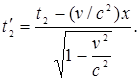
Таким образом, 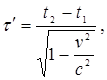или ,

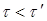т.е. длительность события, происходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, относительно которой эта точка неподвижна. Следовательно, часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоящихся часов, т.е. ход часов замедляется в системе отсчета, относительно которой часы движутся.

3. Длина тел в разных системах отсчета. Рассмотрим стержень, расположенный вдоль оси x΄ и покоящийся относительно системы К΄. Длина стержня в системе К΄ равна 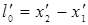, где 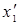, 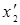- не изменяющиеся со временем t΄ координаты начала и конца стержня; индекс 0 показывает, что в системе К΄ стержень покоится. Определим длину стержня в системе К, относительно которой он движется со скоростью v. Для этого необходимо измерить координаты концов стержня х₁ и х₂ в системе К в один и тот же момент времени t. Их разность и даст длину стержня в системе К:

-

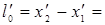
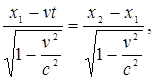
т.е.

Таким образом, размер тела, движущегося относительно инерциальной системы отсчета, уменьшается в направлении движения в раз, т.е. лоренцево сокращение длины тем больше, чем больше скорость движения.

4. Релятивистский закон сложения скоростей. Пусть материальная точка движется в системе К΄ вдоль оси x΄, а система К΄ движется относительно К со скоростью v (оси х и x΄ совпадают). Тогда

Произведя вычисления, получим релятивистский закон сложения скоростей:

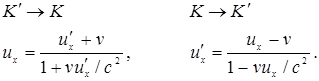
Если скорости v, малы по сравнению со скоростью света, то эти формулы переходят в привычный закон сложения скоростей в классической механике. Релятивистский закон сложения скоростей не противоречит второму постулату Эйнштейна: если 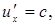то 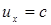, т.е. скорость с – предельная скорость, которую невозможно превысить.

5.4. Основной закон релятивистской динамики.

Релятивистская энергия

Согласно представлениям классической механики, масса тела есть величина постоянная. Однако в конце XIX в. на опытах с электронами было установлено, что масса тела зависит от скорости его движения, а именно возрастает с увеличением v по закону

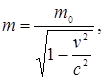(5.8)

где - масса покоя, т.е. масса материальной точки, измеренная в той инерциальной системе отсчета, относительно которой точка покоится; m – масса точки в системе отсчета, относительно которой она движется со скоростью v.

Из принципа относительности Эйнштейна, утверждающего инвариантность всех законов природы при переходе от одной инерциальной системы отсчета к другой, следует, что основной закон динамики Ньютона

оказывается инвариантным по отношению к преобразованиям Лоренца, если в нем справа стоит производная от релятивистского импульса:

(5.9)

или

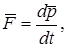(5.10)

где

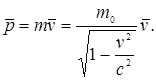(5.11)

Из приведенных формул следует, что при скоростях, значительно меньших скорости света в вакууме, они переходят в формулы классической механики. Следовательно, условием применимости законов классической механики является условие 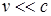. Законы Ньютона получаются как следствие СТО для предельного случая 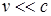. Таким образом, классическая механика – это механика макротел, движущихся с малыми (по сравнению со скоростью света в вакууме) скоростями.

Вследствие однородности пространства в релятивистской механике выполняется закон сохранения релятивистского импульса: релятивистский импульс замкнутой системы тел сохраняется, т.е. не изменяется с течением времени.

Изменение скорости тела в релятивистской механике влечет за собой изменение массы, а, следовательно, и полной энергии, т.е. между массой и энергией существует взаимосвязь. Эту универсальную зависимость – закон взаимосвязи массы и энергии – установил А. Эйнштейн:

(5.13)

Из (5.13) следует, что любой массе (движущейся m или покоящейся ) соответствует определенное значение энергии. Если тело находится в состоянии покоя, то его энергия покоя

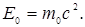
Энергия покоя является внутренней энергией тела, которая складывается из кинетических энергий всех частиц, потенциальной энергии их взаимодействия и суммы энергий покоя всех частиц.

В релятивистской механике не справедлив закон сохранения массы покоя. Именно на этом представлении основано объяснение дефекта массы ядра и ядерных реакций.

В СТО выполняется закон сохранения релятивистской массы и энергии: изменение полной энергии тела (или системы) сопровождается эквивалентным изменением его массы:

(5.14)

Таким образом, масса тела, которая в классической механике является мерой инертности или гравитации, в релятивистской механике является еще и мерой энергосодержания тела.

Физический смысл выражения (5.14) состоит в том, что существует принципиальная возможность перехода материальных объектов, имеющих массу покоя, в электромагнитное излучение, не имеющее массы покоя; при этом выполняется закон сохранения энергии.

Классическим примером этого является аннигиляция электрон-позитронной пары и, наоборот, образование пары электрон-позитрон из квантов электромагнитного излучения:

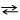
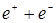
В релятивистской динамике значение кинетической энергии Е_к определяется как разность энергий движущегося Е и покоящегося Е ₀ тела:

(5.15)

При 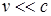уравнение (5.15) переходит в классическое выражение

Из формул (5.13) и (5.11) найдем релятивистское соотношение между полной энергией и импульсом тела:

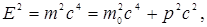
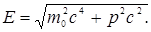(5.16)

Закон взаимосвязи массы и энергии полностью подтвержден экспериментами по выделению энергии при протекании ядерных реакций. Он широко используется для расчета энергического эффекта при ядерных реакциях и превращениях элементарных частиц.

Краткие выводы

· Специальная теория относительности – это новое учение о пространстве и времени, пришедшее на смену классическим представлениям. В основе СТО лежит положение, согласно которому никакая энергия, никакой сигнал не может распространяться со скоростью, превышающей скорость света в вакууме. При этом скорость света в вакууме постоянна и не зависит от направления распространения. Это положение принято формулировать в виде двух постулатов Эйнштейна – принципа относительности и принципа постоянства скорости света.

· Область применения законов классической механики ограничена скоростью движения материального объекта: если скорость тела соизмерима со скоростью света, то необходимо использовать релятивистские формулы. Таким образом, скорость света в вакууме является критерием, определяющим границу применимости классических законов, т.к. она является максимальной скоростью передачи сигналов.

· Зависимость массы движущегося тела от скорости движения определяется соотношением

· Релятивистский импульс тела и соответственно уравнение динамики его движения

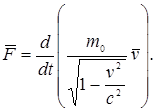
· Изменение скорости в релятивистской механике влечет за собой изменение массы, а, следовательно, и полной энергии:

· В СТО выполняется закон сохранения релятивистской массы и энергии: изменение полной энергии тела сопровождается эквивалентным изменением ее массы:

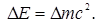
Физический смысл этого соотношения заключается в следующем: существует принципиальная возможность перехода материальных объектов, имеющих массу покоя, в электромагнитное излучение, не имеющее массы покоя; при этом выполняется закон сохранения энергии. Это соотношение является важнейшим для ядерной физики и физики элементарных частиц.

Вопросы для самоконтроля и повторения

1. В чем заключается физическая сущность механического принципа относительности? Чем отличается принцип относительности Галилея от принципа относительности Эйнштейна?

2. Каковы причины создания специальной теории относительности?

3. Сформулируйте постулаты специальной теории относительности.

4. Запишите преобразования Лоренца. При каких условиях они переходят в преобразования Галилея?

5. В чем заключается релятивистский закон сложения скоростей?

6. Как в релятивистской механике масса движущегося тела зависит от скорости?

7. Запишите основное уравнение релятивистской динамики. Чем оно отличается от основного закона ньютоновской механики?

8. В чем заключается закон сохранения релятивистского импульса?

9. Как выражается кинетическая энергия в релятивистской механике?

10. Сформулируйте закон взаимосвязи массы и энергии. В чем его физическая сущность?

Примеры решения задач

Задача 1. Ионизированный атом, вылетев из ускорителя со скоростью 0,8 с, испустил фотон в направлении своего движения. Определить скорость фотона относительно ускорителя.

Дано:

Найти:

Дата добавления: 2013-12-13