Дифференциал функции

Лекция № 11, ВАС-11, 1 сем, 2012

Тема. Дифференциал функции одной переменной, его геометрический смысл. Использование дифференциала функции в приближенных вычислениях. Производная функции, заданной параметрически.

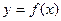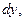Определение 1.1. Пусть функция имеет в точке x производную Тогда величина определяемая выражением

(1.1)

называется дифференциалом функции. Величина называется дифференциалом аргумента x.

Обычно дифференциал аргумента обозначается символом 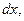поэтому равенство (1.1) записывается в виде:

(1.1^*)

Представим геометрический смысл дифференциала (рис. 1.1).

Рис. 1.1

Рисунок (рис. 1.1) иллюстрирует данное определение. Отрезок – это приращение аргумента, отрезок – это приращение функции, отрезок – это дифференциал функции Из рисунка 1.1 следует: но , поэтому равенство является геометрической записью равенства (1.1^*):

Дифференциал аргумента равен его приращению, , дифференциал функции приближенно равен приращению функции, соответствующему , . Это приближение тем более точно, чем меньше величина .

Для иллюстрации применения формул (1.1) и (1.1^*) на практике рассмотрим следующую задачу.

Задача 1.1. Найти дифференциал функции

и вычислить его значение при следующих значениях 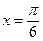и 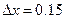и сравнить полученное значение 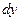с приращением функции .

Решение. Найдем дифференциал данной функции по формуле (2.1):

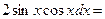
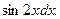
Подставим в полученное выражение числовые данные:

Вычислим приращение функции .

;

.

Разность между и , величина , равна:

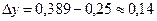и

Ответ. , .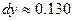

Из рис. 1.1 и из решения задачи 1.1 следует, что Однако дифференциал 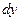тем меньше отличается от величины чем меньше величина . С уменьшением этой величины модуль разности 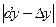уменьшается значительно быстрее, чем модуль , и при достаточно малых значениях можно принять: . Поэтому дифференциал функции (1.1) можно использовать при вычислении приближенного значения функции 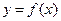в случае небольшого изменении аргумента, используя формулу:

,

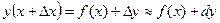или

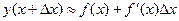(1.2)

Покажем, как это делается на практике.

Задача 1.2. Найти значение величины , не пользуясь калькулятором.

Решение. Воспользуемся формулой (1.2), полагая 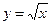, 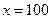и .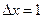

,

Ответ.

Достаточно точное значение корня равно: , и отличается от полученного нами значения приблизительно на 0.001%.

Дата добавления: 2013-12-13