
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Эквивалентные бесконечно малые функции
|
|
|
|
Доказательство.
Натуральный логарифм
Наряду с экспонентой в математике и ее приложениях играет натуральный логарифм.
Натуральным логарифмом называется логарифм с основанием e – эйлеровым числом, обозначаемый символом  .
.
Справедливо утверждение. Функция 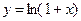 обладает следующим свойством:
обладает следующим свойством:
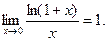 (3.1)
(3.1)


Задача 3.1. Найти предел функций:
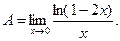
Решение. Имеем неопределенность вида:
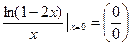 .
.
Для ее раскрытия введем новую переменную 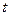 по формуле
по формуле 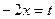 ,
,  . Очевидно,
. Очевидно, 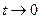 при
при 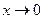 . Отсюда получаем:
. Отсюда получаем:
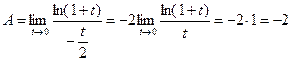 .
.
Эквивалентные бесконечно малые функции играют в теории пределов большую роль: они значительно облегчают вычисления пределов отношения бесконечно малых функций.
Определение 4.1. Две бесконечно малые функции 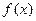 и
и  называются эквивалентными при
называются эквивалентными при 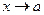 , если предел их отношения при
, если предел их отношения при 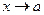 равен единице:
равен единице:
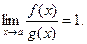 (4.1)
(4.1)
Эквивалентность функций обозначается символом «~» или «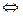 ». Из равенства (1.1) следует:
». Из равенства (1.1) следует: 
Например, функции 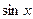 и
и 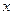 эквивалентны при
эквивалентны при 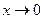 ,
,  т.к.
т.к. 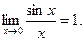
Другие примеры эквивалентных функций дают равенства:
10. 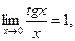 20.
20. 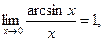 30.
30. 
40. 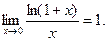
Приведем список эквивалентных бесконечно малых функций, применяемых на практике.
Важнейшие эквивалентности, используемые
при вычислении пределов при 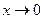
10.  60.
60. 
20. 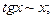 70.
70. 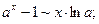
30.  80.
80. 
40. 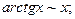 90.
90. 
50.  100.
100. 
В раскрытии неопределенностей типа  большую пользу оказывает следующая теорема.
большую пользу оказывает следующая теорема.
Теорема 4.1. Предел отношения двух бесконечно малых функций не изменится, если одну из них или каждую заменить эквивалентной ей бесконечно малой функцией.
Доказательство. Имеем две пары бесконечно малых функций:
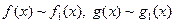 при
при  (4.2)
(4.2)
Докажем справедливость равенства:
 (4.3)
(4.3)
Для доказательства преобразуем дробь в левой части равенства (1.3):


Воспользуемся свойством пределов – предел произведения функций равен произведению пределов эти х функций:

и окончательно:
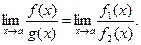
Теорема доказана.
Покажем, как используя доказанную теорему, упростить решение задач лекции № 3.
Задача 4.1. Найти предел функций:
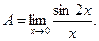
Решение. Имеем неопределенность вида  . Раскроим эту неопределенность:
. Раскроим эту неопределенность:
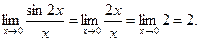
Задача 4.2. Найти предел функций:
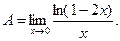
Решение. Имеем неопределенность вида  . Раскроим ее:
. Раскроим ее:

Рассмотрим решение более сложных задач.
Задача 4.3. Найти предел функций:

Решение. Очевидно, здесь неопределенность типа 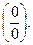 Для ее раскрытии применим теорему об эквивалентных БМФ.
Для ее раскрытии применим теорему об эквивалентных БМФ.


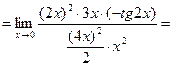
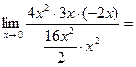
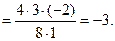
Задача 4.4. Найти предел функций:
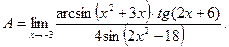
Решение. Подставим в числитель и знаменатель дроби 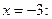
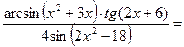
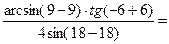
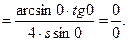
Неопределенность вида 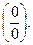
Применим теорему об эквивалентности БМФ:


Задача 4.5. Найти предел функций:

Решение. Имеем неопределенность типа 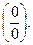
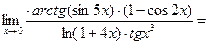

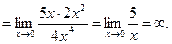
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 3804; Нарушение авторских прав?; Мы поможем в написании вашей работы!