Модель умного водителя. Модель Трайбера

Модель Умного Водителя — для автомобиля a описывает его положение в момент времени t и скорости Va описывает величина xa. Далее, величина la задает длину автомобиля.

Стандартная модель оптимальной скорости обладает рядом недостатков. В частности, она очень чувствительна к конкретному выбору функциональной зависимости оптимальной скорости от дистанции v^/_e(d_n), а также к выбору ΐ. При больших значениях ΐ в модели начинают происходить столкновения автомобилей, в то время как при слишком малых значениях возникают нереалистично большие ускорения.

На самом деле характерные времена разгона приблизительно в пять раз превышают характерные времена торможения. Кроме того, в реальности водители выдерживают большую дистанцию и тормозят раньше при высокой скорости относительно лидера ∆v_n(t). Для учета этих и других особенностей реального поведения водителей было разработано много вариантов модели.

Одной из наиболее удачных микромоделей можно признать модель «разумного водителя» (Intelligent Driver Model, IDM), разработанную Трайбером.

Калибровка и численные эксперименты с этой моделью показали, что ее свойства устойчивы к вариации параметров; модель демонстрирует реалистическое поведение при разгоне и торможении и воспроизводит основные наблюдаемые свойства транспортного потока.

В модели IDM предполагается, что ускорение автомобиля является непрерывной функцией скорости v_n, «чистой» дистанции до лидера s_n = d_n - l_n-1 и скорости относительно лидера ∆vn:

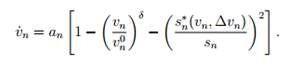
Слагаемое a_n[1 - (v_n/v⁰_n)δ] в правой части этого уравнения описывает динамику ускорения автомобиля на свободной дороге, в то время как слагаемое f_n,n-1 =a_n[s*_n(vn, ∆v_n)/s_n]² описывает торможение, связанное со взаимодействием с лидером. Выбор параметра δ позволяет откалибровать поведение, связанное с разгоном.

Значение δ = 1 соответствует экспоненциальному по времени разгону, характерному для большинства других моделей. При увеличении этого параметра ускорение не убывает экспоненциально в процессе разгона (в пределе при δ→ ∞ происходит разгон с постоянным ускорением a_n вплоть до достижения желаемой скорости v⁰_n), что лучше соответствует поведению водителей. Тормозящий член зависит от отношения «желаемой» дистанции s*_n и фактической дистанции s_n, причем желаемая дистанция дается выражением

Параметры модели могут быть выбраны индивидуально для каждого n-го автомобиля, что позволяет учесть индивидуальные характеристики водителей и транспортных средств. Однако многие общие характеристики потока могут быть получены из рассмотрения идентичных водителей. Параметры имеют содержательную интерпретацию, это — желаемая скорость v₀, безопасный временной интервал T, максимальное ускорение a, «комфортное» (не экстренное) торможение b, показатель «чувствительности» при ускорении «заторные» дистанции s^/ и s^// и длина автомобиля l. Для сокращения числа параметров можно упростить модель, положив δ = 1, s^// = 0 и l = 0, при этом адекватность модели в значительной степени сохраняется.

В равновесном потоке, когда ϋ_n = 0 и ∆v_n = 0, водители стремятся сохранить зависящую от скорости равновесную дистанцию до лидера s_e(v) = s*(v; 0)[1 –(v/v0)^δ]^1/2. Из этого соотношения можно найти равновесную скорость и построить фундаментальную диаграмму. В частности, в специальном случае, когда δ = 1 и s^/ = s^// = 0, можно найти аналитическое выражение для равновесной скорости

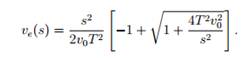
Из этого выражения и очевидного соотношения, связывающего дистанцию с плотностью автомобилей s = (d- l) = (1/ρ- l) = (1/ρ- l/ρ max), получаем равновесный поток Q_e(ρ) = ρV_e(ρ) как функцию плотности, т.е. фундаментальную диаграмму.

Коэффициент δ влияет на форму диаграммы таким образом, что при росте δ переход от свободного к загруженному режиму становится более резким. В пределе при δ→ ∞ и s^// = 0 фундаментальная диаграмма становится треугольной с углом в точке максимального потока: Q_e(ρ) = min(ρv₀, [1- ρ(l+s^/)]=T). При уменьшении δ форма кривой сглаживается, приближаясь к наблюдаемой.

Дата добавления: 2013-12-13