Закон Фурье, коэффициент теплопроводности

Основные понятия, используемые при описании процессов переноса тепла.

Температурное поле – совокупность значений температуры во всех точках изучаемого пространства в данный момент времени. Математически оно записывается в виде

t = f (x, y, z, τ).

Нахождение температурного поля является главной задачей аналитической теории теплопроводности.

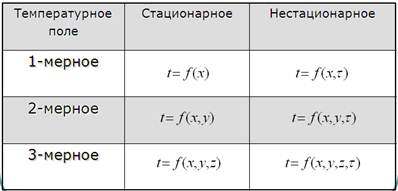
Различают стационарное температурное поле, когда температура во всех точках пространства не зависит от времени, и нестационарное, соответствующее неустановившемуся процессу. В зависимости от количества координат, вдоль которых может изменяться температура тела, различают одномерное, двухмерное и трехмерное поля температур.

Изотермическая поверхность – геометрическое место точек, температура которых одинакова.

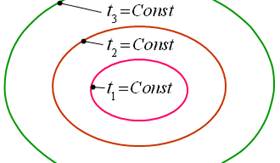
Так как одна и та же точка пространства не может одновременно иметь разные значения температуры, то изотермические поверхности не могут пересекаться. Они либо оканчиваются на поверхности тела, либо целиком лежат внутри тела (не могут обрываться внутри тела).

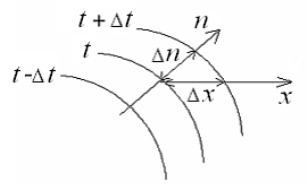
На рис. 1 изображено семейство изотерм, отличающихся на Δ t. Температура в теле может изменяться только в направлениях, пересекающих изотермические поверхности. Наибольший перепад температуры на единицу длины происходит в направлении нормали к изотермической поверхности.

Рис. 1

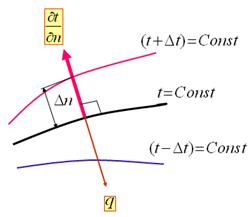
Градиент температуры grad (t) – вектор, направленный по нормали к изотермической поверхности в сторону возрастания температуры и численно равный производной от температуры по этому направлению. Градиент температуры – это предел отношения возрастания температуры между изотермическими поверхностями к расстоянию между ними по нормали, К/м:

Градиент температуры – это вектор, нормальный (перпендикулярный) к изотермической поверхности и направленный в сторону возрастания температуры.

Необходимым условием распространения тепла является неравномерность распределения температуры в рассматриваемой среде, поэтому для передачи тепла теплопроводностью необходимо неравенство нулю температурного градиента в различных точках тела.

В сторону противоположную градиенту температуры направлено падение температуры и тепловой поток. Тепловой поток Q – количество теплоты, передаваемое в единицу времени через произвольную поверхность. Тепловой поток – это вектор, нормальный к изотермической поверхности, направленный в сторону убывания температуры.

Плотность теплового потока (удельный тепловой поток) q – тепловой поток, отнесенный к единице поверхности. Это вектор, совпадающий с направлением распространения тепла, т.е. направлен в сторону убывания температуры и ортогонален изотермам.

Исследуя процесс теплопроводности в твердых телах, Фурье экспериментально установил (1822 г.), что количество переданного тепла пропорционально времени, площади сечения, перпендикулярного направлению распространения тепла, и градиенту температуры:

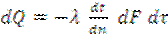(1)

где λ – множитель пропорциональности, называемый коэффициентом теплопроводности, который является физическим параметром, характеризует способность данного вещества проводить тепло и численно равен количеству теплоты, переданному в единицу времени через единицу поверхности при градиенте температуры, равном единице.

Разделив правую и левую части уравнения (1) на время и площадь поверхности, получим наиболее распространенную формулировку закона Фурье: плотность теплового потока пропорциональна градиенту температуры. Физический смысл λ представлен на рис. 2.

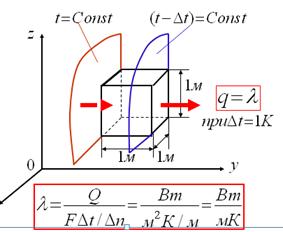
Рис. 2 Физический смысл λ

Коэффициент теплопроводности, характеризующий способность данного вещества проводить тепло, в общем случае зависит от структуры, плотности, влажности, давления и температуры. В технических расчетах значения коэффициента теплопроводности берутся из справочных таблиц, в которых, как правило, учитывается зависимость коэффициента теплопроводности от температуры. Большинство этих табличных данных получено в результате измерения теплового потока и градиента температуры в заданном веществе из определения коэффициента теплопроводности:

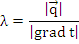
Перенос тепла теплопроводностью в газах при обычных давлениях и температурах определяется переносом кинетической энергии теплового движения в результате хаотического движения и столкновения отдельных молекул газа. С изменением давления коэффициент теплопроводности меняется незначительно, а с ростом температуры он увеличивается. Исключением является водяной пар, теплопроводность которого падает с ростом температуры, для которого к тому же проявляется значительная зависимость от давления. Для смесей газов правило аддитивности не действует, коэффициент теплопроводности определяется опытным путем. Для газов значение коэффициента теплопроводности лежит в диапазоне 0,005–0,5 Вт/(м К). Самые высокие значения коэффициента теплопроводности имеют водород и гелий.

Механизм распространения тепла в капельных жидкостях можно представить как перенос энергии путем нестройных упругих колебаний. С повышением температуры убывает плотность жидкости и коэффициент теплопроводности (за исключением воды и глицерина), с повышением давления – увеличивается. Для жидкостей коэффициент теплопроводности не превышает 1 Вт/(м К) и лежит примерно в диапазоне 0,07–0,7 Вт/(м К).

В металлах переносчиками тепла являются электроны, которые можно уподобить идеальному одноатомному газу. Вследствие движения электронов происходит выравнивание температуры во всех точках нагревающегося или охлаждающегося металла. Свободные электроны движутся во всех направлениях – как из более нагретых областей в холодные, так и в обратном направлении. В первом случае они отдают энергию атомам, а во втором – отбирают.

Так как в металлах носителями тепловой и электрической энергии являются электроны, то коэффициент теплопроводности и электропроводность пропорциональны друг другу. При повышении температуры вследствие усиления тепловых неоднородностей рассеивание электронов усиливается. Это влечет за собой уменьшение коэффициентов теплопроводности и электропроводности чистых металлов. Примеси значительно снижают коэффициент теплопроводности, так как структурные неоднородности сильно рассеивают электроны. Например, у чистой меди λ=395 Вт/(м К), а у меди с примесями мышьяка λ = 142 Вт/(м К). Для сплавов, в отличие от чистых металлов, коэффициент теплопроводности увеличивается с ростом температуры. В целом коэффициент теплопроводности убывает с уменьшением плотности. Наибольшим коэффициентом теплопроводности обладают чистые серебро и медь (около 400 Вт/(м К)), затем идут золото (300 Вт/(м К)) и алюминий (210 Вт/(м К)). В среднем коэффициент теплопроводности металлов лежит в диапазоне 20–400 Вт/(м К).

В неметаллических твердых телах коэффициент теплопроводности растет с увеличением температуры, а также с ростом плотности вещества. Здесь на величину коэффициента теплопроводности оказывают влияние структура, пористость и влажность материала. Многие строительные материалы являются пористыми, а применение закона Фурье к пористым материалам условно. Его следует понимать следующим образом: такой коэффициент теплопроводности имело бы сплошное тело таких же формы и размеров, а также температурах на границе при прохождении через него такого же количества тепла. Для порошкообразных и пористых тел коэффициент теплопроводности сильно зависит от их объемной плотности – растет с ее увеличением, так как теплопроводность заполняющего поры воздуха существенно меньше теплопроводности твердых компонентов пористого материала С ростом влажности коэффициент теплопроводности пористых материалов увеличивается в первую очередь за счет конвективного переноса тепла из-за капиллярного движения воды. Для неметаллических твердых материалов коэффициент теплопроводности обычно ниже 10 Вт/(м К), для строительных и теплоизоляционных материалов составляет 0,02–3,0 Вт/(м К).

Дата добавления: 2013-12-13