Математическая формулировка задач теплопроводности. Дифференциальное уравнение теплопроводности

Изучение любого физического явления сводится к установлению зависимости между величинами, характеризующими это явление. При решении задач, связанных с нахождением температурного поля, необходимо иметь дифференциальное уравнение теплопроводности.

В основу вывода дифференциального уравнения теплопроводности положен закон сохранения энергии: количество тепла dQ, введенное в элементарный объем dv извне за время d τ вследствие теплопроводности, а также от внутренних источников тепла, равно изменению внутренней энергии вещества, содержащегося в этом объеме:

dQ ₁ + dQ ₂ = dQ,

где dQ ₁ – количество тела, введенное в элементарный объем dv путем теплопроводности за время dτ;

dQ ₂ – количество тепла, которое за время dτ выделилось в элементарном объеме dv за счет внутренних источников тепла;

dQ –изменение внутренней энергии вещества, содержащегося в элементарном объеме dv за время dτ. Тогда

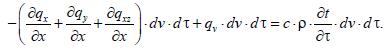
Выразим частную производную от температуры по времени:

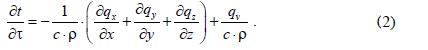
Плотность теплового потока в соответствии с законом Фурье равна q = -λ grad t. Проекции вектора плотности теплового потока на соответствующие координатные оси определим как q_x=-λ 𝜕t/𝜕x, q_y=-λ 𝜕t/𝜕y, q_z=-λ 𝜕t/𝜕z Подставим эти выражения в (2) и получим:

Если обозначить через оператор Лапласа =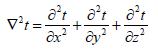

a = λ/(c 𝜌) – коэффициент температуропроводности, то дифференциальное уравнение теплопроводности (3) можно записать как

Коэффициент температуропроводности характеризует скорость изменения температуры в нестационарных процессах, является мерой теплоинерционных свойств тела. Скорость изменения температуры будет тем выше, чем больше коэффициент температуропроводности, т.е. при прочих равных условиях выравнивание температуры будет происходить быстрее. Также коэффициент температуропроводности зависит от природы вещества: для металлов больше, чем для жидкостей и газов.

В цилиндрической системе координат оператор Лапласа имеет вид

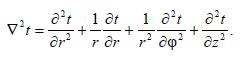
3 Краевые условия задач теплопроводности, различные способы задания граничных условий. Закон Ньютона – Рихмана

Дифференциальное уравнение теплопроводности (3) выведено на основе общих законов физики и описывает процесс теплопроводности в самом общем виде. Любое дифференциальное уравнение описывает целый класс явлений. Для того, чтобы выделить конкретный рассматриваемый процесс и дать его полное математическое описание, к дифференциальным уравнениям надо присоединить математическое описание всех частных особенностей рассматриваемого процесса. Эти частные особенности, которые совместно с дифференциальным уравнением дают полное математическое описание конкретного процесса теплопроводности, называются условиями однозначности или краевыми условиями и включают:

1) геометрические условия, характеризующие форму и размеры тела, в котором протекает процесс;

2) физические условия, характеризующие физические свойства тела (теплопроводность, теплоемкость, плотность, мощность внутренних источников тепла и т.д.);

3) временные или начальные условия, характеризующие распределение температуры в изучаемом теле в начальный момент времени: при τ = 0 t = f(x,y,z);

4) граничные условия, характеризующие взаимодействие рассматриваемого тела с окружающей средой.

Граничные условия могут быть заданы несколькими способами.

Граничные условия первого рода, в которых задается распределение температуры на поверхности тела для каждого момента времени: t _c = f(x, y, z, τ); частный случай t _c = const.

Граничные условия второго рода, в которых задается величина теплового потока для каждой точки поверхности тела и для любого момента времени: q _c = f(x, y, z, τ); частный случай q _c = const. Например, нагревание металлических изделий в высокотемпературных печах.

Граничные условия третьего рода, в которых задается температура окружающей среды t _ж и закон теплообмена между поверхностью тела и окружающей средой в процессе охлаждения и нагревания. Для его описания используется закон Ньютона – Рихмана: плотность теплового потока пропорциональна разности температур поверхности тела t _c и окружающей среды t _ж:

q = α (t _c – t _ж).

Здесь α – коэффициент теплоотдачи, характеризующий интенсивность теплообмена между поверхностью тела и окружающей средой. Численно равен количеству тепла, отдаваемому (воспринимаемому) единицей поверхности в единицу времени при разности температур между поверхностью и средой в один градус.

По закону сохранения энергии количество тепла, отводимое с единицы поверхности вследствие теплоотдачи, должно равняться теплу, подводимому к единице поверхности вследствие теплопроводности из внутренних объемов тела, тогда

Граничные условия четвертого рода характеризуют теплообмен системы тел или тела с окружающей средой по закону теплопроводности (идеальный контакт):

Таким образом, дифференциальное уравнение совместно с условиями однозначности дают полную математическую формулировку конкретной задачи теплопроводности, которая может быть решена аналитически, численно, экспериментально.

Дата добавления: 2013-12-13