Ошибки частного

1). Абсолютная ошибка частного D_ч равна произведению относительной ошибки d _ч частного на его величину:

D_ч = d _ч .

2). Относительная ошибка частного равна сумме относительных ошибок делимого и делителя:

d _ч = d ₁ + d ₂.

Частное вида a/N, где N – безошибочное число, имеет абсолютную ошибку в N раз меньшую, чем ошибка D _а:

D_ч = .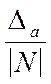

Ошибка степени. Если приближенное число а возводится в п -ю степень, то:

1). Абсолютная ошибка степени D_ст равна относительной ошибке d_а числа, умноженной на модуль произведения степени а^п и ее показателя п:

D_ст = d_а .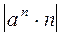

2). Относительная ошибка степени вычисляется по формуле:

d _ст = d_а.

Ошибки корня. Очевидно D_к = d_а и d _к = d_а/п.

Приведенные выше формулы составлены так, что при вычислениях по ним, как правило, происходит накопление ошибок, в то время как фактически в процессе расчетов ошибки приближенных чисел в значительной степени компенсируются.

Обычно ошибки промежуточных результатов не подсчитываются. Чтобы обеспечить достаточную точность конечного результата, рекомендуется придерживаться следующих правил подсчета необходимого количества знаков[1]:

1. При сложении и вычитании приближенных чисел результат должен содержать столько десятичных знаков, сколько их имеет число с наименьшим количеством таких знаков.

2. При умножении и делении приближенных чисел результат должен состоять из стольких значащих цифр, сколько их имеет число с наименьшим количеством таких цифр.

3. При возведении приближенного числа в квадрат или куб должно быть сохранено такое количество значащих цифр, какое их имеет возводимое в степень число, например, 1,1² = 1,21≈1,2

4. При извлечении квадратного или кубического корня результат должен быть выражен таким количеством значащих цифр, сколько их в подкоренном числе.

Лишние знаки числа исчисляются путем округления. Его производят по правилам, называемым правилами дополнения:

· Когда первая из отбрасываемых цифр меньше пяти, последнюю из оставляемых цифр не изменяют, например, 2,39724» 2,3972;

· Когда первая отбрасываемая цифра больше пяти, последний сохраняемый знак числа увеличивают на единицу: 0,09186» 0,0919;

· Когда первая отбрасываемая цифра равна пяти, а последующие знаки – нули, то последнюю оставляемую цифру не изменяют, если она выражается четным числом, и увеличивают на единицу, если – нечетным (округление до четного числа): 513,0 2 50» 513,02; 78,2 3 50» 78,24;

· При наличии после отбрасываемой пятерки значащих цифр, отличных от нуля, последнюю из оставляемых цифр следует увеличить на единицу: 8419,3853» 8419,39.

Соблюдение этих правил дополнения обеспечивает округление чисел с ошибкой, не превышающей 0,5 единицы разряда последнего оставляемого в числе знака. Ошибка эта имеет положительный знак при округлении с избытком и отрицательный – при округлении с недостатком.

В ходе вычислений округление промежуточных результатов надо выполнять, сохраняя вместе с верными одну сомнительную цифру. Но конечный результат округляется так, чтобы все цифры числа были верными. (Верная цифра – абсолютная погрешность приближения <=единицы того разряда, которому принадлежит эта цифра.)

При проведении вычислений на ЭВМ, всегда следует помнить, что результаты вычислений в подавляющем большинстве случаев являются приближенными, т.к. они содержат целый ряд погрешностей. Мерой точности вычислений может служить либо абсолютная, либо относительная погрешность.

При этом все источники погрешности вычислений можно разделить на три группы:

1. Неустранимая погрешность. Погрешность, возникающая за счет неточности исходных данных, называется неустранимой. Исходные данные, полученные решения в результате измерений или каких-либо вычислений, обязательно содержат погрешности. Эти погрешности преобразуются в конечный результат решения задачи.

Пример. S _кв. = а², а – носитель неустранимой ошибки.

Если известны предельные погрешности исходных данных, то по установленным правилам можно оценить погрешность результата вычислений, но устранить ее нельзя.

2. Погрешность округления. В процессе вычислений производят округление чисел, получающихся в результате действий. Нередко округляют и исходные данные. Погрешность, возникающую при округлении чисел, называют погрешностью округления.

Погрешности округления при решении задач на ЭВМ обусловлены конечной длиной машинных слов, обрабатываемых на ЭВМ.

3. Погрешности метода и модели. При математической постановке задачи оказываются неучтенными различные особенности изучаемого явления. Зачастую это определяется тем, что введение уточняющих членов приводит к значительным усложнениям математической модели, в том числе и таким, при которых модель становится непригодной для вычислений.

Ошибки могут быть обусловлены погрешностями самого метода решения задачи.

Пусть величина и определяется формулой u = f(x, y, …). Требуется вычислить u по исходным данным х, у, ….

Может оказаться, что непосредственное применение данной формулы затруднительно или невозможно. Заменяя формулу u = f(x, y, …) другой формулой u = φ(x, y, …), применение которой позволяет облегчить процесс вычислений и дает результат, достаточно близкий к результату вычислений по первой формуле.

Выполняя вычисления по второй формуле, получаем приближенный результат даже в том случае, если исходные данные взяты точными, и все промежуточные вычисления производились точно.

Погрешность метода – это погрешность, возникающая в результате замены одного математического процесса (не обязательно вычисления по формуле) другим.

Простейшим примером таких вычислений являются вычисления с помощью приближенных формул.

Чтобы оценить точность результата, следует проанализировать весь вычислительный процесс, т.е. найти полную погрешность, которая складывается из погрешности метода и модели, неустранимой погрешности и погрешности округления.

Если Δ' – погрешность метода и модели,

Δ'' – неустранимая погрешность,

Δ''' – погрешность округления,

то полная погрешность

Δ и = Δ'+ Δ''+ Δ'''.

При вычислении следует учитывать распространение ошибок. Ошибка, возникшая на входе вычислительного алгоритма или в определенном месте в ходе вычислений, распространяется дальше. Влияние ошибки на результат по мере выполнения последующих операций может увеличиваться или уменьшаться.

Например, при вычитании почти равных чисел относительная ошибка может оказаться очень большой. Эта большая ошибка будет распространяться дальше при выполнении всех последующих операций.

На всех этапах решения задачи на ЭВМ необходимо заботиться о том, чтобы гарантировать необходимую точность полученного результата.

Для этого существуют определенные рекомендации:

1. выражения, предназначенные для вычислений, следует преобразовать таким образом, чтобы свести к минимуму число необходимых арифметических операций;

2. если нужно выполнить сложение-вычитание длинной последовательности чисел, сначала выполняются действия с наименьшими числами;

3. на промежуточных этапах следует избегать вычитания почти равных чисел.

Алгоритм называется устойчивым, если в процессе его работы вычислительные погрешности возрастают незначительно, и неустойчивым ‑ в противном случае. При использовании неустойчивых вычислительных алгоритмов накопление погрешностей вычисления приводит в процессе счета к переполнению арифметического устройства компьютера.

Дата добавления: 2013-12-13