Композиция (произведение) преобразований

Геометрические преобразования плоскости и пространства. Определение преобразований множеств. Примеры. Композиция (произведение) преобразований. Группа преобразований.

Лекция №22.

1.Преобразование множества.

Биективное отображение множества на себя называется преобразованием этого множества. Преобразование множества X иногда называют подстановками,чаще всего это принято, если X-конечно.

Пример 1.

На множестве Q (Q-либо плоскость π, либо пространство E³), возьмём точку O отображение:

Z₀:Q Q,

зададим следующим образом:

1) (∀: А, А ≠ 0) (А^| = Z₀ (А)) ó (А^| ∈ [AO) ∧ АО = ОА^|);

где [АО) – луч.

Z₀

2) 0 0

Покажем, что Z₀ –преобразование Q.Для этого достаточно доказать, что Z₀ – биекция.

Z₀ – инъекция, так-как истина предложения

(∀: A,B)(A ≠ B) Z₀ (A) ≠ Z₀ (B).

Очевидно,что Z₀ – сюръекция,так-как ∀ M^| ∈ Q рассмотрев, как образ можем по указанному правилу найти преобразование M.

Это преобразование называется центральной симметрией (плоскости или пространства).

Пример 2.

На плоскости π возьмём прямую l.

S_l: π π –зададим следующим образом:

1) (∀: A ∉ l)(А^|=S_l (А) ó(АА^| ┴ l ∧ АО = ОА^|, О = l ⋂ А^| A);

2) (∀ B, B ∈ l) (S_l (B) = B) – это преобразование называется оси ось симметрии. l – ось.

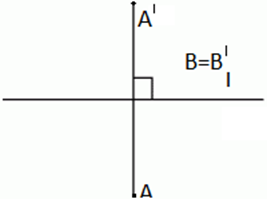
Пример 3.

В пространстве Е³ возьмём плоскость π.Отображение:

S_п: Е³ Е³ , зададим следующим образом:

1)(∀: A, А ∉ π) (А^| = S_п (А))↔(АA^| ┴ π ∧ AO=OA^|, О= π ∧ A^| A);

2)(∀: В, В ∈ π) (S(B)=B)

Легко доказать, что S_П – преобразующая пространства.

S_п называется симметрией относительно плоскости.

Пример 4.

В пространстве Е³ возьмём прямую l, отображение S_l: Е³ Е³ зададим следующим образом:

1)(∀: A,A ∉ l) (А^| =S_l(А)↔(ОА┴ l, О=l ⋂ АА^|,АО=ОА^|);

2)(∀: В; В ∈ l) (В=S_l (В)).

Не трудно доказать, что S_l преобразование.

S_l называется симметрией пространства относительно прямой.

Пример 5.

На множестве Q (Q либо плоскость, либо трёхмерное пространство). Возьмём направленный отрезок MN; φ: Q Q зададим следующим образом:

(∀: A) (φ (А) =А^|) ↔ АА^| = МN, где МN -вектор определяемый отрезком

МN.

Покажем, что φ есть преобразующая Q, то есть биекция. В самом деле инъективность следует из того, что из любой точки С можно провести единственную прямую | | МN. И на луче из точки С в данном направлении можно отложить единственный отрезок имеющий длину равную МN.

Сюръективность следует из того, что ∀: точек А^| плоскости можно найти точку А для которой А^| является образом при соотношении φ. Такую точку найдём из условия А^|А МN и А^|А=NМ. Это преобразование называется параллельным переносом множеством Q определяемым направленным

отрезком МN =а, Т_а (или Т _МN).

Пример 6.

Пусть на ориентированной плоскости π дана точка О. Далее пусть α – величина некоторого ориентированного угла. Отображение R_o^α: π → π, зададим следующим образом:

1)(∀: A; А ≠ О)(А = R_o(А))↔(ОА, ОА^|)=α, АО=ОА^|);

2)R_o^α (O)=O

Можно доказать, что R_o^α - преобразование. Это преобразование называется поворотом вокруг точки О на угол α.

j

o A^|

i α

O A

Пример 7.

Пусть Е³ – ориентированное пространство, l - некоторая прямая, α – величина ориентированного угла. Рассмотрим отображение R_l^α: E^3→E³, заданное правилом:

1)(∀: A, А ∉ l)(А^| =R_l^α(А))↔((О ∈ l, l ┴ (О,А,А^|)), ОА=ОА^|, (ОА,ОА^|)=α);

2)(∀: B; В ∈ l)(R_l^α(В)=В) - легко доказать, что R_l^α преобразование,Е³ называется поворотом пространства вокруг оси l.

Пример 8.

Отображение е: Q →Q зададим следующим образом: (∀: M ∈ Q)(e(M)=M) – это преобразование называется тождественным преобразованием множества Q, то есть плоскости или пространства.

Пусть f и q – два преобразующих множества X, считаем, что f=q на множестве X, если ∀ x ∈ X справедливо равенство f(x)=q(x).

Пусть f и q два преобразующих множества Х, отображаются φ:Х Х заданным правилом.

(∀x ∈ X)(φ(x)=q(f(x), называется композицией преобразований f и q.

φ=q o f

Лемма 1.

Композиция преобразований множества Х есть преобразование этого множества.

Замечание:

Композиция преобразований в общем случае не коммутативна.

Пример 1.

На плоскости π возьмём 2 пересекающиеся прямые d и l. Пусть f - симметрия относительно d. S_l = q; q – симметрия относительно l. Возьмём некоторую точку М, тогда (fq)(M) ≠ (qf)(M)→fq ≠ qf

M d

(f ◦ g)(M)

f (M) l

(g ◦ f) M

N

Пример 2.

Пусть f и q – параллельные переносы, определяемые соответствующими векторами а и b плоскости или пространства, тогда f ◦ q – параллельный перенос Т_{b + a}

g ◦ f – параллельный перенос Т _{а + b}

Так как b + а = a + b, то Т _{b + а} = Т _{a + b} = 1 в этом случае f ◦ q = q ◦ f

Теорема 1.

Пусть F = { f } множество всех преобразований множества Х, тогда для любых преобразований f, q, h множества Х справедливы:

1)f(qh)=(fq)h – ассоциативность композиции.

2)fe=ef=f;

3)f^-1 - преобразование множества Х.

f◦f^-1 = f^-1◦f = e

Дата добавления: 2013-12-13