Маркированные потоки

Альтернирующие потоки

Расстояния между соседними точками потока не обязательно одинаково распределены. Распределения могут чередоваться. Например, возьмем две последовательности случайных величин: ξ₁, ξ₂,... и η₁, η₂,... и положим

x_2n = ξ₁ +... + ξ_n + η₁ +... + η_n, x_2n−1 = ξ₁ +... + ξ_n + η₁ +... + η_n−1.

Тогда построение потока на всей прямой делается, как и выше. В нашем случае чередуются длины автомобилей di (независимые и одинаково распределенные) и функции d⁺_i (независимые и одинаково распределенные).

Каждой точке x_i точечного процесса может быть сопоставлена величина σi, принимающая значения в некотором множестве S. Эту величину в разных случаях называют маркой или спином в точке i и говорят о случайном маркирован ном точечном множестве (потоке, процессе). Он определяется мерой на последовательностях пар (x_i, σ_i). Проще всего, когда задана мера на счетных множествах, то есть задан поток без марок, а величины σi объявляются независимыми и одинаково распределенными. Построим маркированный процесс, где марками являются скорости, причем их распределение будет сложным образом коррелировать во времени с траекториями точек.

Эволюция во времени конфигураций автомобилей часто использует марковские процессы, и необходимо сказать о соответствующей терминологии. Часто определение самого процесса и его свойств (например, эргодичности) отличаются в разных источниках. Поясним это. Для простоты ограничимся случаем дискретного времени.

Рассмотрим на некотором фазовом пространстве X систему мер (переходных вероятностей) P(A|x), определяющих вероятности того, что в момент t+1 процесс попадет в множество A ⊂ X, если в момент t процесс находился в состоянии x ∈ X. Если все меры P(A|x) одноточечные, то это эквивалентно заданию детерминированного отображения T: X → X, точнее P(.|x) = δ(T(x)) — единичная мера в точке T(x). Тогда говорят о детерминированном отображении, задающем динамическую систему.

Заметим, что система мер P(A|x) определяет очевидным образом преобразование U множества вероятностных мер на X в себя:

.

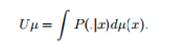Важным является понятие инвариантной (относительно U) меры. Обычно исследуется ее существование, единственность и другие свойства.

По системе переходных вероятностей можно построить разные последовательности случайных величин ξn со значениями в X или их распределений µn на X, где P(ξ_n ∈ A) = µ_n(A). Вероятностным пространством при этом служит множество траекторий {x_n}. Например, по вероятностной инвариантной мере строится стационарный марковский процесс как последовательность ξ_n, n ∈ Z+ случайных величин со значениями в X. Или по заданной начальной мере µ0 на X строится последовательность ξ_n, n ∈ Z₊.

Под марковским процессом может пониматься как одна из таких последовательностей случайных величин, так и все семейство таких последовательностей ξ_n. Соответственно разнится терминология, например, определение эргодичности. Динамическая система с заданной инвариантной мерой µ называется эргодической, если любое инвариантное множество имеет меру µ ноль или единицу. На любой стационарный марковский процесс можно смотреть как на динамическую систему — сдвиг в пространстве траекторий. Тогда понятие эргодичности совпадает с понятием эргодичности этой динамической системы.

Однако чаще, когда говорят о марковском процессе, имеют в виду не только стационарные процессы. Наиболее часто используемым определением эргодичности является следующее. Процесс называется эргодическим, если существует единственная инвариантная мера µ на X, и для любой начальной меры µ0 при n → ∞ имеет место слабая сходимость µ_n → µ.

Отметим, что марковские процессы резко разделяются на два класса. Первый класс — для которых существует положительная мера на X (не обязательно вероятностная), относительно которой все меры P(.|x) абсолютно непрерывны. К ним относятся почти все классические марковские процессы — конечные и счетные цепи Маркова, диффузионные процессы и другие. Такие процессы называются эргодическими, если, во-первых, у преобразования нет нетривиальных инвариантных множеств, а во-вторых, существует единственная инвариантная вероятностная мера. Во многих случаях отсюда следует сходимость к этой инвариантной мере из любого начального распределения. Для счетных цепей эквивалентным условием является положительная возвратность, то есть конечность (для всех пар x, y ∈ X) среднего времени достижения y из x.

Второй класс характеризуется тем, что все меры P(.|x) взаимно сингулярны. К этому классу относятся почти все процессы с бесконечным числом частиц. Теория таких процессов существенно сложнее.

Дата добавления: 2013-12-13