Случайная динамика с обгоном (случайные грамматики)

Случайная динамика без обгона

То же самое получится, если скорости v одинаковы, функции d ⁺_i случайны и независимы, а их средние равны (для заданного v) некоторому числу d⁺(v). Мы видим, что сам факт нетривиальной зависимости пропускной способности от скорости тривиален, и для него совершенно не нужны вероятностные модели. Однако для более тонких вопросов вероятностные модели необходимы. Сейчас мы введем довольно общую вероятностную модель с очень богатым спектром фаз. При этом процессы с запретами (exclusion processes) появляются как вырожденный частный случай.

Здесь естественно возникает связь с таким недавно открытым объектом, как случайные грамматики. Мы дадим краткое содержательное описание одной такой модели.

Пусть в момент t = 0 все автомобили находятся на левой полуоси, движение однополосное. Мы разбиваем полосу движения на клетки определенной длины и считаем, что в каждой клетке не более одного автомобиля. Таким образом, конечная последовательность автомобилей изображается парой (S, r), где r ∈ Z, а S — конечная последовательность (слово) из трех символов 0, 1, 2:

S = s_N...s₂s₁

При этом 0 соответствует пустой клетке, 1 — активному (быстрому) водителю в клетке, 2 — спокойному водителю в клетке. Длина слова N = N(t) и все символы s_k(t) могут меняться во времени, но так, что всегда s₁(t) ≠ 0 для всех t ≥ 0. В произвольный момент t каждый символ sk(t) имеет координату x(s_k(t)). Координаты однозначно определяются

x(s_k(t)) = x(s₁(t)) − k + 1

координатой x(s₁(t)) первого символа, которую мы обозначим r = r(t).

Динамика моделирует процесс ускорений и торможений отдельных водителей и определяется как цепь Маркова (S(t), r(t)) с непрерывным временем на множестве пар {(S, r)}. Интенсивности скачков определяются так. Изменения S и r независимы друг от друга. Изменение r моделирует движение всего потока с постоянной скоростью v. Именно, r увеличивается на единицу с вероятностью vdt за время dt, и все координаты немедленно изменяются соответственно формуле. Динамика S, таким образом, будет описывать ситуацию относительно некоторого равномерного движения. Эта динамика задается случайной грамматикой, то есть списком возможных локальных замен подслов (всего будет 5 типов замен) S на другое подслово.

Любые замены из приводимого ниже списка производятся независимо, случайно и имеют разные интенсивности (всего 4 параметра). Вот этот список.

1) 10 → 01 — быстрый водитель передвигается на 1-го вперед, освобождая свободное место за собой, с вероятностью λ⁺₀dt за время dt;

2) 120 → 021 — быстрый водитель обгоняет спокойного, с вероятностью λ⁺₁dt;

3) 22 → 202, 21 → 201 — предусмотрительный водитель тормозит, увеличивая дистанцию перед собой, с вероятностью λ⁻₂dt. Отметим, что здесь увеличивается длина S (возникает лишняя свободная ячейка), что ведет к сдвигу всех автомобилей сзади этого водителя на 1-го назад. Это нелокальный скачок, реально он растянут во времени, но это совместимо с правилом сложения относительных скоростей;

4) 200 → 020 — спокойный водитель ускоряется с вероятностью λ⁺₂dt (если впереди с его точки зрения много свободного места).

Необходимо сказать, что для точной формулировки результатов, которые мы лишь обрисуем, надо делать разнообразные скейлинги параметров t, N, λ. Это будет сделано в отдельной статье. В зависимости от 4 параметров могут быть разнообразные типы (фазы) движения. Мы приведем только три из них.

Если λ±2 малы по сравнению с остальными двумя параметрами, то автомобили типа 2 едут синхронно и с постоянной скоростью, а быстрые автомобили имеют дополнительную относительную скорость. Если быстрых автомобилей мало, то эта дополнительная скорость определяется движением одного автомобиля среди неподвижных препятствий и зависит от плотности ρ₂ автомобилей типа 2 и плотности дырок ρ0 и примерно равна

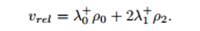
Если λ−2 мала по сравнению с остальными двумя параметрами (нет нелокальных эффектов), а λ+2 имеет такой же порядок как λ+0, λ+1, то разница между типами стирается. Мы имеем тогда процесс, близкий к так называемому полностью асимметричному процессу с запретами (TASEP — totally asymmetric exclusion process), а для значений полностью с ним совпадающий.

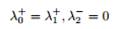
Если λ⁺₂ мала, а λ⁻₂велика по сравнению с остальными двумя параметрами, то картина иная. Каждый обгон 120 → 021 вызывает немедленное торможение автомобиля 2 и, как следствие, все последующие автомобили замедляются. Для автомобилей ближе к концу слова замедление будет весьма существенным, если поток достаточно плотный (мало ячеек с нулями), так как много автомобилей типа 2 будет тормозиться.

Можно усложнять введенную динамику, например, избежать дискретизации, вводя вместо нулей положительные вещественные числа — расстояния между последовательными автомобилями. Это потребует существенных переформулировок, особенно для скачков типа 3, но сохранит грубые качественные эффекты.

Дата добавления: 2013-12-13