Булевы выражения

Импликация

Идемпотентность (отсутствие степеней коэффициентов)

Х*Х = Х

X v X = Х

6. Закон двойного отрицания (инволюционный закон):

Х = Х

7. Свойства констант 0 и 1:

X * 1 = X;	X v 1 = 1;
X * 0 = 0;	X v 0 = X;
0 = 1;	1 = 0;

8. Закон де Моргана:

Х1*Х2 = Х1 v Х2;

Х1 v Х2 = Х1 * Х2;

9. Закон противоречия:

Х*Х = 0

10. Закон исключения третьего:

Х v Х = 1

11. Поглощение:

Х v X*Y = X

12. Склеивание:

X*Y v X*Y = X;

Х v X*Y = X v Y

А®В = А v B

Булево (булевское) выражение - это выражение, которое содержит булевы константы, переменные, логические операции. Порядок выполнения операций определяется их приоритетом, для изменения порядка выполнения операций используются скобки.

Одна и та же логическая функция может быть записана различным образом. Например, функция F(x1, x2) может быть записана следующими эквивалентными выражениями:

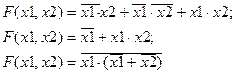
Эквивалентность выражений легко проверить подстановкой в них значений х1 и х2, или с помощью логических преобразований. Для исключения неоднозначности записи логические функции представляют в унифицированных формах. Такими формами являются дизъюнктивная и конъюнктивная. В них используются элементарные дизъюнкции и конъюнкции.

Элементарной конъюнкцией называется конъюнкция, в которую входят только переменные или их отрицания.

Например,

.

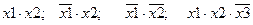Элементарной дизъюнкцией называется дизъюнкция, представляющая собой логическую сумму переменных или их отрицаний.

Например,

.

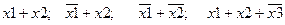В элементарные дизъюнкции и конъюнкции не могут входить одинаковые переменные, а так же переменные с их отрицаниями. Такие дизъюнкции и конъюнкции должны преобразовываться. При этом они упрощаются или обращаются в 0 или 1.

Элементарные дизъюнкции и конъюнкции характеризуются рангом, равным количеству переменных в дизъюнкции или конъюнкции. Понятия элементарных дизъюнкции и конъюнкции позволяют достаточно просто определить дизъюнктивную и конъюнктивную формы записи логических функций.

Дизъюнктивная нормальная форма (ДНФ) – это форма, в которой логическая функция представляется в виде дизъюнкции элементарных конъюнкций.

Например,

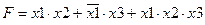
Конъюнктивной нормальной формой (КНФ) – называется такая форма, в которой логическая функция представляется в виде конъюнкции элементарных дизъюнкций.

Например,

.

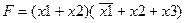И все же, использование нормальных форм не устраняет полностью неоднозначности записи логических функций.

Например,

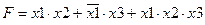
Может быть записана так:

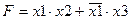
Среди нормальных форм выделяют такие, в которых функции записываются единственным образом. Их называют совершенными. Применяются совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ). Они имею две отличительные особенности:

1. все элементарные конъюнкции и дизъюнкции имеют одинаковый ранг;

2. в элементарные конъюнкцииили дизъюнкции входят все те переменные или их отрицания, от которых зависит функция.

Например,

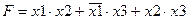записана в ДНФ, а не в СДНФ, хотя все элементарные конъюнкции имеют одинаковый ранг, но запись каждой из них не содержит всех переменных или их отрицаний, от которых зависит функция.

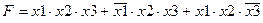записана в СДНФ, т.к. все элементарные конъюнкции имеют одинаковый ранг, и запись каждой из них содержит все переменных или их отрицания, от которых зависит функция.

Предположим, что необходимо описать работу некоторого устройства ‑ "черного ящика", т.е. выразить выход F как функцию входных переменных х1, х2, … хn.:

х1
х2
…	F
хn

х1, х2, … хn – набор булевых переменных – вход.

F – логическая функция – выход.

Чтобы описать поведение "черного ящика", необходимо записать булево выражение или построить таблицу истинности.

Дата добавления: 2013-12-13