Волновое уравнение

Лекция №13

Схема “крест”

Гиперболическое волновое уравнение описывает колебания струны, движение сжимаемого газа, распространение электромагнитных волн и ряд других явлений.

Типичной одномерной задачей является задача описания малых колебаний натянутой струны с распределенной по длине нагрузкой f (t, x):

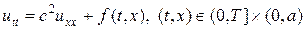; (1)

; (2)

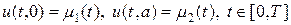. (3)

Уравнение колебания струны (1) дополняется начальными условиями (2), которые, в отличие от параболического уравнения требуют двух условий: начального смещения относительно положения равновесия u ₀(x) и начальную скорость движения u ₁(x). Кроме того, задаются краевые условия (3), которые называются краевыми условиями первого рода, они описывают смещение концов струны относительно положений равновесия. Краевые условия могут быть и иного рода.

Составим несложную, но эффективную разностную схему для численного решения задачи (1) — (3), выбирая для простоты равномерные по t и x сетки. В качестве шаблона разностной схемы возьмем, представленный на рис.1 шаблон в форме “креста”. Аппроксимируя производные в (1) конечными разностями, получим трехслойную схему следующего вида

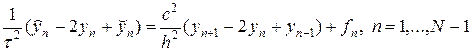, (4)

с граничными условиями

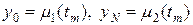. (4¢)

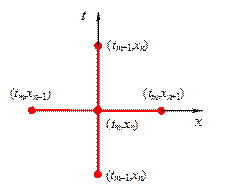
Рис.1. Разностная схема (4) в форме креста

По форме шаблона схему (4) называют схемой “крест”. Исследуем схему крест.

Процедура вычисления решения выглядит следующим образом. На нулевом слое решение известно из начального условия

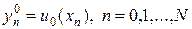. (5)

На первом слое решение можно также вычислить по начальным данным. Простейший способ получения решения на первом слое состоит в аппроксимации второго начального условия в (2) согласно представлению:

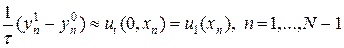. (6)

Аппроксимация (6) имеет первый порядок точности, тогда как в схеме крест разностный оператор второй производной по времени имеет второй порядок точности. Поэтому для более точной аппроксимации необходимо учесть еще один член разложения, т.е.

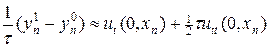. (6¢)

Подставляя в (6¢) u_tt из (1), найдем

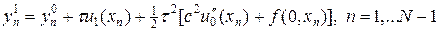. (6¢¢)

Схема крест (4) является явной, поскольку позволяет выразить решение на следующем слое 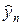через значения y_n и 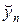на двух предыдущих слоях. Поэтому, зная значения решения на нулевом (5) и первом слое (6¢¢), можно вычислить решения на всех последующих слоях. Итак, разностное решение существует и единственно.

Для изучения аппроксимации схемы крест, разложим точное решение по формуле Тейлора с центром в узле (t_m, x_n), считая все появляющиеся в разложении производные непрерывными:

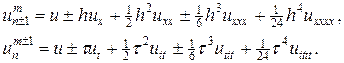
Используя данные разложения, легко можно найти невязку схемы крест:

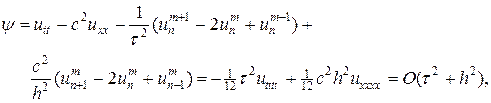(7)

а также невязку начального условия (6):

,

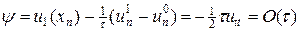или более точного начального условия (6¢¢):

(7¢)

Начальные (2) и краевые условия (3) аппроксимируются точно. В итоге разностная схема (4) с начальными условиями (5), (6¢¢) имеет порядок аппроксимации 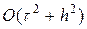, а та же разностная схема с начальным условием (6¢) имеет несколько худший порядок — .

Устойчивость схемы крест исследуем методом разделения переменных, полагая

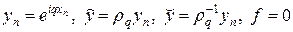. (8)

Подставляя представление (8) в (4), для множителя роста гармоник находим квадратное уравнение

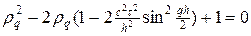. (9)

По теореме Виета произведение корней квадратного уравнения (9) равно единице, т.е. 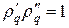. Условие устойчивости 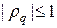может таким образом быть выполнено при 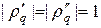. Это означает, что корни уравнения (9) должны образовывать комплексно сопряженную пару. Для этого необходимо, чтобы дискриминант уравнения (9) был неположительным для всех гармоник, т.е.

. (10)

Для выполнения неравенства (10) необходимо и достаточно соблюдение условия Куранта:

ct < h. (11)

В (11) стоит строгое неравенство, т.к., если верно равенство Куранта ct = h для некоторых гармоник, то появляется слабая неустойчивость из-за того, что корень квадратного уравнения (9) становится кратным.

В итоге разностная схема крест (4) с начальными условиями (5), (6¢) при выполнении условия Куранта (11) сходится с порядком аппроксимации 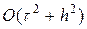. Из наших рассуждений следует, что сходимость имеет место в норме 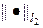. Схема (4) обеспечивает хорошую точность расчета решения u (t, x), имеющих четвертую непрерывную производную. Схема позволяет также рассчитывать и менее гладкие решения.

Изучим аппроксимацию и сходимость схемы крест на численном примере решения уравнения (1) с правой частью, начальными и граничными условиями вида:

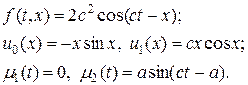(12)

Нетрудно проверить, что решение задачи (1), (12) имеет следующее аналитическое решение:

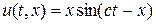. (13)

На листинге_№1 приведен код программы численного решения задачи (1), (12) с помощью разностной схемы крест (4) и начальными условиями (5), (6¢¢), т.е. с порядком аппроксимации .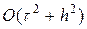

Листинг_№1

%Программа решения волнового уравнения (1), (12) с

%помощью схемы крест (4)

function cross

global c

%Определяем габариты области интегрирования по времени T

%и пространству a, а также параметр c

T=1; a=2*pi; c=1;

%Определяем максимальное число удвоений числа узлов по

%времени и пространству smax

smax=6; N=2;

%Организуем основной цикл расчетов с различными сетками

for s=1:smax

%Определяем число узлов по пространству и удвоенное

%число узлов по времени

N=2*N; M=2*N;

%Определяем шаги по времени и пространству

tau=T/(M-1); h=a/(N-1);

r=(c^2*tau^2)/h^2;

%Определяем сетки по времени и пространству

t=0:tau:T; x=0:h:a;

%Используем начальные данные из (12) для

%определения численного решения на первом и

%втором слое по формуле (6'')

for n=1:N

y(1,n)=-x(n)*sin(x(n));

y(2,n)=y(1,n)+tau*c*x(n)*cos(x(n))+...

0.5*tau^2*(c^2*(-2*cos(x(n))+...

x(n)*sin(x(n)))+f(0,x(n)));

end

%Определяем левое и правое граничные условия,

%взятые из (12)

for m=1:M

y(m,1)=0; y(m,N)=a*sin(c*t(m)-a);

end

%Применяем схему крест (4) к нашей задаче

for m=2:(M-1)

for n=2:(N-1)

y(m+1,n)=2*y(m,n)-y(m-1,n)+r*(y(m,n+1)-...

2*y(m,n)+y(m,n-1))+tau^2*f(t(m),x(n));

end

end

%Оцениваем зависимость предстепенной константы

%const=||y-u||/h^2 ошибки численного решения на

%последнем шаге по времени в норме C от h

for n=1:N

z1(n)=abs(y(M,n)-u(t(M),x(n)));

end

const(s)=max(z1)/h^2;

step(s)=h;

end

mi=0;

for m=1:5:M

mi=mi+1; ti(mi)=t(m); ni=0;

for n=1:5:N

ni=ni+1; xi(ni)=x(n); z(mi,ni)=y(m,n);

end

end

%Рисуем трехмерную поверхность решения в координатах

%время-пространство

subplot(1,2,1); surf(xi,ti,z);

%Рисуем график зависимости предстепенной константы от

%шага сетки

subplot(1,2,2); loglog(step,const);

%Определяем функцию правой части

function y=f(t,x)

global c

y=2*c^2*cos(c*t-x);

%Определяем аналитическое решение

function y=u(t,x)

global c

y=x*sin(c*t-x);

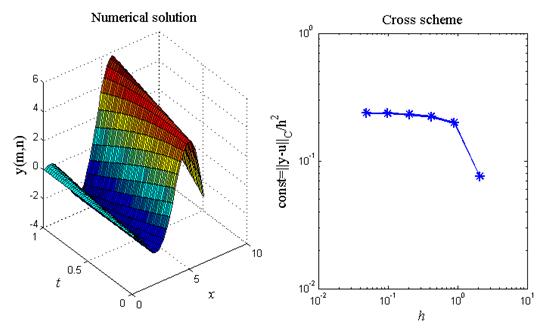
Рис.2. Численное решение волнового уравнения (1), (12) с помощью
схемы крест (4), (5), (6¢¢)

На рис.2 приведен итог работы кода программы листинга_№1. На левом рисунке приведен внешний вид численного решения 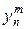, m = 1,…, M. На правом рисунке приведена зависимость предстепенной константы const в представлении зависимости ошибки численного решения 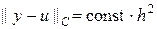от шага сетки, при этом шаг по времени выбирался порядка шага по пространству (при выполнении условия Куранта), т.е. t ~ h. Видно, что по мере уменьшения шага h величина const действительно выходит на некоторое постоянное значение, что подтверждает второй порядок аппроксимации 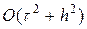схемы крест (4) с начальными условиями (5), (6¢¢).

Дата добавления: 2013-12-13