Статистическая оценка параметров распределения

Оценка - это приближение значений искомой величины, полученное на основании результатов выборочного наблюдения. Оценки являются случайными величинами. Они обеспечивают возможность формирования обоснованного суждения о неизвестных параметрах генеральной совокупности. Примером оценки генеральной средней является выборочная средняя генеральной дисперсии – выборочная дисперсия и т.д.

Для того чтобы оценить насколько «хорошо» оценка отвечает соответствующей генеральной характеристике разработаны 4 критерия: состоятельность, несмещенность, эффективность и достаточность. Этот подход основывается на том, что качество оценки определяется не по ее отдельным значениям, а по характеристикам ее распределения как случайной величины.

Основываясь на положениях теории вероятностей, можно доказать, что из таких выборочных характеристик, как средняя арифметическая, мода и медиана, только средняя арифметическая представляет собой состоятельную, несмещенную, эффективную и достаточную оценку генеральной средней. Этим и обуславливается предпочтение, отдаваемое средней арифметической в ряду остальных выборочных характеристик.

Несмещенность оценки проявляется в том, что ее математическое ожидание при любом объеме выборки равно значению оцениваемого параметра в генеральной совокупности. Если это требование не выполняется, то оценка является смещенной.

Условие несмещенности оценки направлено на устранение систематических ошибок оценивания.

При решении задач оценивания применяют также асимптотически несмещенные оценки, для которых при увеличении объема выборки математическое ожидание стремится к оцениваемому параметру генеральной совокупности.

Состоятельность статистических оценок проявляется в том, что с увеличением объема выборки оценка все больше и больше приближается к истинному значению оцениваемого параметра или, как говорят, оценка сходится по вероятности к искомому параметру, или стремится к своему математическому ожиданию. Лишь состоятельные оценки имеют практическую значимость.

Эффективная оценка – это такая оценка несмещенного параметра, которая обладает наименьшей дисперсией при данном объеме выборки. На практике дисперсия оценки обычно отождествляется с ошибкой оценки.

В качестве меры эффективности оценки принимают отношение минимально возможной дисперсии к дисперсии другой оценки.

Оценка, обеспечивающая полноту использования всей содержащейся в выборке информации о неизвестной характеристике генеральной совокупности, называется достаточной (исчерпывающей).

Соблюдение рассмотренных выше свойств статистических оценок дает возможность считать выборочные характеристики для оценки параметров генеральной совокупности лучшими из возможных.

Важнейшая задача математической статистики состоит в том, чтобы по выборочным данным получить наиболее рациональные, «правдивые» статистические оценки искомых параметров генеральной совокупности. Различают два вида статистических выводов: статистическая оценка; проверка статистических гипотез.

Основная задача получения статистических оценок заключается в выборе и обосновании наилучших оценок, обеспечивающих возможность содержательной оценки неизвестных параметров генеральной совокупности.

Задача оценки неизвестных параметров может быть решена двумя способами:

1) неизвестный параметр характеризуется одним числом (точкой) - используется метод точечной оценки;

2) интервальная оценка, то есть определяется интервал, в котором с некоторой вероятностью может находиться искомый параметр.

Точечная оценка неизвестного параметра заключается в том, что конкретное числовое значение выборочной оценки принимается за наилучшее приближение к истинному параметру генеральной совокупности, то есть неизвестный параметр генеральной совокупности оценивается одним числом (точкой), определенным по выборке. При таком подходе всегда существует риск совершить ошибку, поэтому точечная оценка должна дополняться показателем возможной ошибки при определенном уровне вероятности.

В качестве средней ошибки оценки принимается ее среднее квадратическое отклонение.

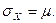
Тогда точечная оценка генеральной средней может быть представлена в виде интервала 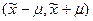где 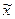- выборочная средняя арифметическая.

При точечной оценке применяют несколько методов получения оценок по выборочным данным:

1) метод моментов, при котором моменты генеральной совокупности заменяются моментами выборочной совокупности;

2) метод наименьших квадратов;

3) метод максимального правдоподобия.

Во многих задачах требуется найти не только числовую оценку параметра генеральной совокупности, но и оценить ее точность и надежность. Особенно это важно для выборок относительно малого объема. Обобщением точечной оценки статистического параметра является его интервальная оценка – нахождение числового интервала, содержащего с определенной вероятностью оцениваемый параметр.

В связи с тем, что при определении генеральных характеристик по выборочным данным всегда присутствует некоторая ошибка, практичнее определить интервал с центром в найденной точечной оценке, внутри которого с некоторой заданной вероятностью находится истинное искомое значение оцениваемого параметра генеральной характеристики. Такой интервал называют доверительным.

Доверительный интервал – это числовой интервал, который с заданной вероятностью γ накрывает оцениваемый параметр генеральной совокупности. Такую вероятность называют доверительной. Доверительная вероятность γ - это вероятность, которую можно признать достаточной в рамках решаемой задачи для суждения о достоверности характеристик, полученных на основе выборочных наблюдений. Величину α = 1 – γ вероятности допустить ошибку называют уровнем значимости.

Для выборочной (точечной) оценки Θ^* (тета) параметра Θ генеральной совокупности с точностью (предельной ошибкой) Δ и доверительной вероятностью γ доверительный интервал 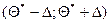определяется равенством:

Доверительная вероятность γ дает возможность установить доверительные границы 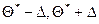случайного колебания изучаемого параметра Θ для данной выборки.

В качестве доверительной вероятности принимают зачастую следующие значения и соответствующие им уровни значимости α = 1 – γ:

Таблица 3.1 - Наиболее употребительные доверительные вероятности и уровни значимости

Вероятность, γ	Уровень значимости, a
0,90	0,10 или 10 %
0,95	0,05 или 5 %
0,99	0,01 или 1 %

Например, 5-процентный уровень значимости означает следующее: в 5-ти случаях из 100 существует риск совершить ошибку при выявлении характеристик генеральной совокупности по выборочным данным. Или, другими словами, в 95 случаях из 100 генеральная характеристика, выявленная на основе выборки будет лежать в пределах доверительного интервала.

Дата добавления: 2013-12-13