Статистическая оценка выборки

Теоретической основой выборочного метода являются теория вероятностей и закон больших чисел. При случайном отборе единиц выборочной совокупности среднее значение изучаемого признака (доли) в выборочной совокупности стремится к характеристикам генеральной совокупности, то есть по величине среднего значения признака (доли) в выборочной совокупности можно судить о среднем значении этого признака (доли) в генеральной совокупности. Однако, вследствие наличия ошибок репрезентативности, значения генеральной и выборочной средней (доли) всегда различаются на величину ошибки выборки, которая не превосходит величины предельной ошибки выборки.

Предельную ошибку обычно представляют в виде

Δ = tμ,

где μ – средняя (стандартная) ошибка выборки,

t – коэффициент, связанный с доверительной вероятностью (коэффициент доверия), определяемый на основе интеграла Лапласа по заданной доверительной вероятности γ (см. Приложение 7):

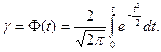
Величина средней ошибки выборки зависит от объема выборки и объема генеральной совокупности (для бесповторной выборки) и соответствующих дисперсий, которые на практике обычно заменяют их выборочными оценками. Формулы для вычисления средней ошибки выборки разнятся в зависимости от вида выборки. Наиболее часто используемые из них приведены в табл. 3.2.

Способ формирования выборки	Средняя ошибка выборочной средней	Предельная ошибка выборочной средней
Случайный повторный
Случайный бесповторный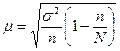
Механический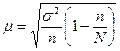
Типический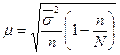
Серийный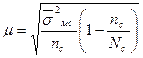

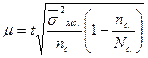
где: μ – средняя ошибка выборки (репрезентативности);

∆х – предельная ошибка выборочной средней;

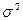– дисперсия признака в генеральной совокупности;

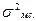– межсерийная дисперсия;

t – кратность ошибки;

n – численность выборки (n_i – типической, n_c – серийной);

N – численность генеральной совокупности (N_i – типической,

N_c – серийной);

– обследованная часть совокупности (доля выборки);

– необследованная часть совокупности.

Следует указать, что приведенные формулы являются некоторыми приближениями средних ошибок, так как в них соответствующие характеристики генеральной совокупности (например, генеральная дисперсия) заменены их выборочными оценками. Однако в большинстве практических задач такая замена неизбежна, так как требуемые параметры генеральной совокупности, как правило, неизвестны. А выборочное обследование может быть направлено на их оценку.

Для получения оценок с заданными точностью (Δ) и вероятностью (γ) требуется сформировать выборочную совокупность объема n (для собственно-случайной, механической и типической выборок) и m (для серийной), не меньшего некоторого числа, то есть определить минимальный объем выборки, при котором обеспечивается оценка с требуемыми свойствами. Формулы для определения необходимого объема для различных выборок следуют из соответствующих формул, представленных в табл. 3.2.

Способ формирования выборки	Необходимая численность выборки
Случайный повторный
Случайный бесповторный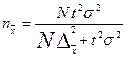
Механический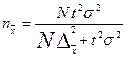
Типический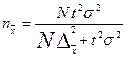
Серийный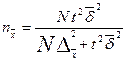

где: ∆х – предельная ошибка выборочной средней;

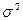– дисперсия признака в генеральной совокупности;

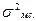– межсерийная дисперсия;

t – кратность ошибки;

n – численность выборки (n_i – типической, n_c – серийной);

N – численность генеральной совокупности (N_i – типической,

N_c – серийной);

– обследованная часть совокупности (доля выборки);

– необследованная часть совокупности.

Следует иметь в виду, что числа, определяемые формулами табл. 3.3, как правило, не являются целыми, поэтому, чтобы получить величину объема выборки (целое число), необходимо к целой части полученного числа прибавить единицу, например, если получено 55,34, то объем равен 56, если 78,99, то 79.

Дата добавления: 2013-12-13