
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Тейлора. Задача.Дана функция , имеющая производных в окрестности точки
|
|
|
|
Задача. Дана функция 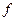 , имеющая
, имеющая 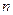 производных в окрестности точки
производных в окрестности точки 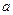 . Подобрать алгебраический многочлен
. Подобрать алгебраический многочлен 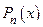 степени
степени 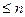 такой, что
такой, что  .
.
Решение. Это − многочлен 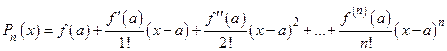 , в краткой записи
, в краткой записи 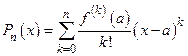 . Многочлен
. Многочлен  называется n-м многочленом Тейлора функции
называется n-м многочленом Тейлора функции 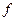 .
.
Доказательство. Ясно, что  . Далее,
. Далее,
 .
.
Поэтому 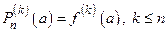 . Ч. и т. д.
. Ч. и т. д.
Замечание 1. Из линейной независимости системы степенных функций 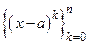 следует единственность решения рассматриваемой задачи.
следует единственность решения рассматриваемой задачи.
Для того, чтобы понять насколько хорошо многочлен Тейлора приближает исходную функцию, необходимо изучить так наз. остаточный член  . Равенство
. Равенство

называют формулой Тейлора с остаточным членом  . Изучим величину
. Изучим величину  .
.
Теорема. Если функция 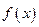 принадлежит классу
принадлежит классу 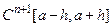 , то есть имеет непрерывные производные прядка
, то есть имеет непрерывные производные прядка 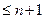 на отрезке
на отрезке  , то для любого
, то для любого 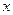 , принадлежащего этому отрезку, существует такое число
, принадлежащего этому отрезку, существует такое число 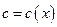 , заключенное между числами
, заключенное между числами 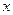 и
и 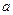 , что остаточный член
, что остаточный член 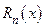 может быть представлен в виде
может быть представлен в виде
 (остаточный член в форме Лагранжа).
(остаточный член в форме Лагранжа).
Доказательство. Положим  . Тогда, очевидно, будет
. Тогда, очевидно, будет  ,
, 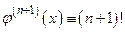 . Кроме того,
. Кроме того,  ,
, 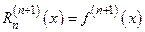 . Применяя многократно теорему Коши о среднем значении, получим
. Применяя многократно теорему Коши о среднем значении, получим



 ,
,
где 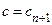 заключено между числами заключено между числами 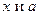 . Доказательство закончено. . Доказательство закончено.
| 
|
Следствие. При тех же условиях можно утверждать, что
 (остаточный член в форме Пеано).
(остаточный член в форме Пеано).
Замечание 2. Если несколько усложнить рассуждения, то можно доказать последнее утверждение при условии, что  существует
существует  (и, разумеется, производные меньших порядков
(и, разумеется, производные меньших порядков  существуют в окрестности этой точки).
существуют в окрестности этой точки).
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 317; Нарушение авторских прав?; Мы поможем в написании вашей работы!