
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Площадь искривленной поверхности
|
|
|
|
Предположим, что поверхность  задана явным уравнением
задана явным уравнением 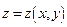 , где
, где 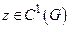 , а
, а  − квадрируемая область, представляющая собой проекцию
− квадрируемая область, представляющая собой проекцию  на плоскость
на плоскость  .
.
Разобьём  на квадрируемые подмножества
на квадрируемые подмножества  и выберём в них по точке
и выберём в них по точке 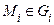 . Обозначим
. Обозначим  точку на поверхности
точку на поверхности  , проецирующуюся
, проецирующуюся  . Рассмотрим касательную плоскость
. Рассмотрим касательную плоскость 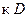 в точке
в точке  и обозначим
и обозначим 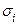 площадь части этой плоскости, проецирующейся
площадь части этой плоскости, проецирующейся  .
.
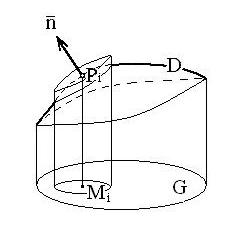
| Так как площадь  , где , где  − угол между касательной плоскостью и плоскостью − угол между касательной плоскостью и плоскостью  , то , то 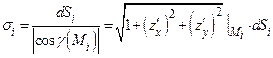 .
Действительно, величина .
Действительно, величина 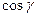 равна третьему направляющему косинусу нормального вектора равна третьему направляющему косинусу нормального вектора  к поверхности к поверхности  в точке в точке  , лежащей над точкой , лежащей над точкой 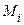 . .
|
Определение. Рассмотрим площадь “описанного многогранника”  .
.
Если существует предел  суммы
суммы 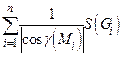 при условии, что мелкость разбиения
при условии, что мелкость разбиения  стремится к нулю, будем считать этот предел площадью поверхности
стремится к нулю, будем считать этот предел площадью поверхности 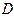 . Ясно, что
. Ясно, что  .
.
Пример. Найти площадь  части параболоида вращения
части параболоида вращения  , отсекаемой плоскостью
, отсекаемой плоскостью  .
.
Решение. 
 =
= .
.
Рассмотрим случай параметрического задания поверхности  с помощью уравнения
с помощью уравнения  ,
,  . Мы будем называть
. Мы будем называть 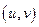 криволинейными координатами на поверхности. Эти координаты называются ортогональными, если
криволинейными координатами на поверхности. Эти координаты называются ортогональными, если 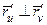 в каждой точке.
в каждой точке.

| Рассмотрим криволинейный “параллелограмм”, заключённый между двумя парами бесконечно близких координатных линий  и линий и линий 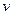 . С точностью до главных бесконечно малых его площадь равна . С точностью до главных бесконечно малых его площадь равна  . Поэтому . Поэтому 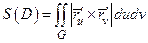 , где , где  − область изменения параметров − область изменения параметров  . .
|
Ясно, что  . Поэтому
. Поэтому
 .
.
Рассмотрим матрицу Грама  для векторов
для векторов  . Это значит
. Это значит 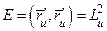 ,
,  ,
,  . Так как
. Так как 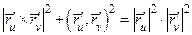 , то
, то 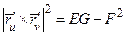 . Поэтому
. Поэтому
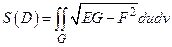 .
.
В частности, если криволинейные координаты на поверхности ортогональные, то 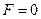 и
и
 .
.
Так, если  − широта и долгота точки, то
− широта и долгота точки, то 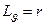 ,
, 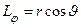 , В этом случае площадь фигуры
, В этом случае площадь фигуры  на сфере
на сфере 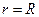 будет равна
будет равна  , где
, где  − область изменения координат
− область изменения координат  .
.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 471; Нарушение авторских прав?; Мы поможем в написании вашей работы!