
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Понятие о несобственных кратных интегралах
|
|
|
|
Физические приложения кратных интегралов.
Массу тела  можно найти по формуле
можно найти по формуле 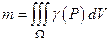 , где
, где  объёмная плотность материала, массу пластины − по формуле
объёмная плотность материала, массу пластины − по формуле  (на этот раз
(на этот раз 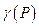 − поверхностная плотность). Точно так же, заряд
− поверхностная плотность). Точно так же, заряд 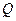 можно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.
можно вычислить, интегрируя объёмную (поверхностную) плотность распределения заряда.
Центр масс: 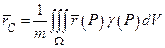 , здесь
, здесь 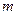 − снова масса тела
− снова масса тела  .
.
Моменты инерции:  ,
, 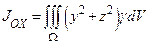 ,
, 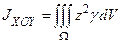 и т.д.
и т.д.
Напряженность в точке  гравитационного поля, создаваемого массой, распределённой с плотностью
гравитационного поля, создаваемого массой, распределённой с плотностью 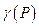 , равна
, равна 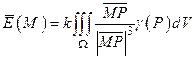 , где
, где  − гравитационная постоянная. Потенциал гравитационного поля равен
− гравитационная постоянная. Потенциал гравитационного поля равен  .
.
Аналогичные формулы справедливы, но со знаком “минус” и  для напряженности и потенциала электростатического поля.
для напряженности и потенциала электростатического поля.
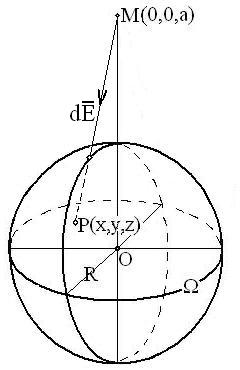
Пример. Доказать, что однородный шар притягивает материальную точку так, как если бы вся масса шара была сосредоточена в его центре.
Решение. Если расположитьшар и точку  так, как показано на рисунке, будет
так, как показано на рисунке, будет 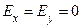 . Вычислим
. Вычислим 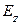 , считая, что
, считая, что 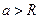 .
.
| 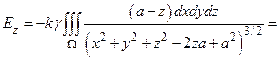
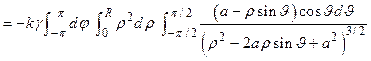 .
Сделаем во внутреннем интеграле следующую замену: .
Сделаем во внутреннем интеграле следующую замену: 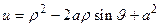 . При этом будет . При этом будет  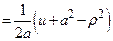 , , 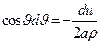 ; ;  . .

 
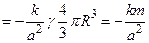 , где , где 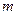 − масса шара. − масса шара.
|
Мы не станем в этом параграфе углубляться в теорию, а рассмотрим лишь один пример: 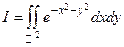 .
.
В этом случае можно дать определение сходимости интеграла по неограниченной области (по всей плоскости) разными способами. Например,
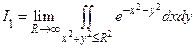 или
или 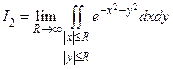 .
.
Докажем, что оба эти предела существуют, конечны и равны между собой.
1. 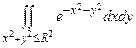 =
=
 .
.
Следовательно,  .
.
2. Так как подынтегральная функция положительна, то интеграл возрастает с расширением области. Поэтому
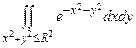
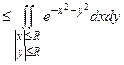
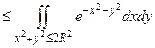 .
.
3. Крайние члены этих неравенств  имеют пределом число имеют пределом число 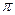 .
По теореме о двух милиционерах средний член также стремится .
По теореме о двух милиционерах средний член также стремится 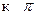 , то есть , то есть 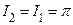 . .
| 
|
Покажем, как воспользоваться эти обстоятельством для вычисления интеграла Пуассона  .
.
Имеем 
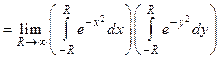 =
=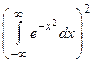 .
.
Поэтому 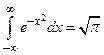 . Отметим, что для теории вероятностей и других дисциплин важным является следствие этой формулы
. Отметим, что для теории вероятностей и других дисциплин важным является следствие этой формулы  .
.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 307; Нарушение авторских прав?; Мы поможем в написании вашей работы!