Понятие корреляции

Взаимосвязи на языке математики обычно описываются при помощи функций, которые графически изображаются в виде линий. На рис. 6.1 изображено несколько графиков функций. Если изменение одной переменной на одну единицу всегда приводит к изменению другой переменной на одну и ту же величину, функция является линейной (график ее представляет прямую линию); любая другая связь — нелинейная. Если увеличение одной переменной связано с увеличением другой, то связь — положительная (прямая); если увеличение одной переменной связано с уменьшением другой, то связь — отрицательная (обратная). Если направление изменения одной переменной не меняется с возрастанием (убыванием) другой переменной, то такая функция — монотонная; в противном случае функцию называют немонотонной.

Функциональные связи, подобные изображенным на рис.1, являются идеализациями. Их особенность заключается в том, что одному значению одной переменной соответствует строго определенное значение другой переменной. Например, такова взаимосвязь двух физических переменных — веса и длины тела (линейная положительная). Однако даже в физических экспериментах эмпирическая взаимосвязь будет отличаться от функциональной связи в силу неучтенных или неизвестных причин: колебаний состава материала, погрешностей измерения и пр.

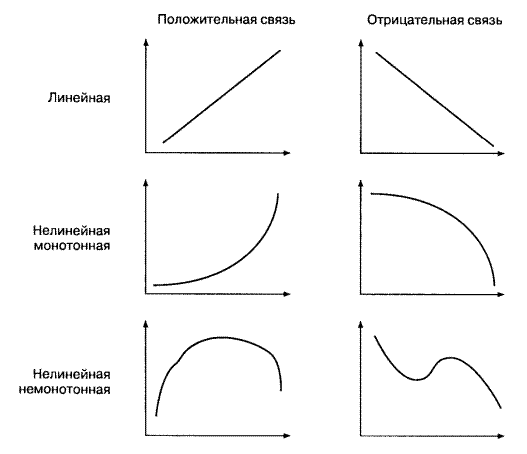
Рис.1 Примеры графиков часто встречающихся функций.

В психологии, как и во многих других науках, при изучении взаимосвязи признаков из поля зрения исследователя неизбежно выпадает множество возможных причин изменчивости этих признаков. Результатом является то, что даже существующая в реальности функциональная связь между переменными выступает эмпирически как вероятностная (стохастическая): одному и тому же значению одной переменной соответствует распределение различных значений другой переменной (и наоборот). Простейшим примером является соотношение роста и веса людей. Эмпирические результаты исследования этих двух признаков покажут, конечно, положительную их взаимосвязь. Но несложно догадаться, что она будет отличаться от строгой, линейной, положительной — идеальной математической функции, даже при всех ухищрениях исследователя по учету стройности или полноты испытуемых. (Вряд ли на этом основании кому-то придет в голову отрицать факт наличия строгой функциональной связи между длиной и весом тела.)

Итак, в психологии, как и во многих других науках, функциональная взаимосвязь явлений эмпирически может быть выявлена только как вероятностная связь соответствующих признаков. Наглядное представление о характере вероятностной связи дает диаграмма рассеивания — график, оси которого соответствуют значениям двух переменных, а каждый испытуемый представляет собой точку (рис. 2). В качестве числовой характеристики вероятностной связи используются коэффициенты корреляции.

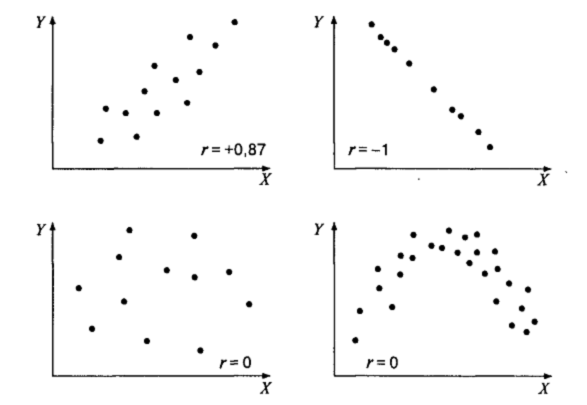
Рис. 2. Примеры диаграмм рассеивания и коэффициентов корреляции.

Коэффициент корреляции — это количественная мера силы и направления вероятностной взаимосвязи двух переменных; принимает значения в диапазоне от —1 до +1.

Сила связи достигает максимума при условии взаимно однозначного соответствия: когда каждому значению одной переменной соответствует только одно значение другой переменной (и наоборот), эмпирическая взаимосвязь при этом совпадает с функциональной линейной связью. Показателем силы связи является абсолютная (без учета знака) величина коэффициента корреляции.

Направление связи определяется прямым или обратным соотношением значений двух переменных: если возрастанию значений одной переменной соответствует возрастание значений другой переменной, то взаимосвязь называется прямой (положительной); если возрастанию значений одной переменной соответствует убывание значений другой переменной, то взаимосвязь является обратной (отрицательной). Показателем направления связи является знак коэффициента корреляции.

Следует отметить еще один важный факт. Когда мы смотрим значение коэффициента корреляции о его значимости можно судить только после того, как мы будем знать объем выборки. Так, одно и то же значение r_xy для одной выборки будет незначимым, а для другой значимым на уровне 0,01. Желающие могут провести следующий эксперимент: для выборки, у которой r_xy оказалось незначимым, надо скопировать ее саму на себя несколько раз. Очевидно, что значение r_xy при этом не изменится, а коэффициент корреляции станет значимым!

КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ r_xy

Дата добавления: 2013-12-13