Частная корреляция

Очень часто две переменные коррелируют друг с другом только за счет того, что обе они согласованно меняются под влиянием некоторой третьей переменной. Иными словами, на самом деле связь между соответствующими свойствами отсутствует, но проявляется в статистической взаимосвязи (корреляции) под влиянием общей причины.

ПРИМЕР

Общей причиной изменчивости двух переменных («третьей переменной») может являться возраст при изучении взаимосвязи различных психологических особенностей в группе детей разного возраста. Предположим, что изучается взаимосвязь между зрелостью моральных суждений — Хн скоростью чтения — К. Но в распоряжении исследователя имеется лишь выборка из 45 детей разного возраста — от 8 до 14 лет (переменная Z— возраст). Если будет получена существенная положительная корреляция между Х и У, например r_xy = 0,54, то о чем это будет свидетельствовать? Осторожный исследователь вряд ли сделает однозначный вывод о том, что зрелость моральных суждений непосредственно связана со скоростью чтения. Скорее всего, дело в том, что и зрелость моральных суждений, и скорость чтения повышаются с возрастом. Иными словами, возраст является причиной согласованной (прямо пропорциональной) изменчивости и зрелости моральных суждений, и скорости чтения.

Для численного определения степени взаимосвязи двух переменных при условии исключения влияния третьей применяют коэффициент частной корреляции (Partial Correlation). Для вычисления частной корреляции достаточно знать три коэффициента корреляции /--Пирсона между переменными X, У и Z: r_xy,r_xz и r_yz):

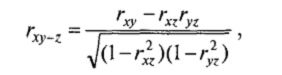
Частная корреляция r_xy-z равна r_xy, при любом фиксированном значении Z (в том случае, если Z линeйнo коррелирует с Х и Y). Например, если значение частной корреляции скорости чтения Х изрелости моральных суждений Ус учетом возраста равно 0,2 (r_xy__z = 0,2) и возраст линейно коррелирует и с Х ис У, то с любой группе детей одного и того же возраста r_xy будет тоже равно 0,2.

9. ФАКТОРНЫЙ И КЛАСТЕРНЫЙ АНАЛИЗ. ФАКТОРНЫЙ АНАЛИЗ.

Возникновение и развитие факторного анализа тесно связано с измерениями в психологии. Длительное время факторный анализ и воспринимался как математическая модель в психологической теории интеллекта. Лишь начиная с 50-х годов XX столетия, одновременно с разработкой математического обоснования факторного анализа, этот метод становится общенаучным. К настоящему времени факторный анализ является неотъемлемой частью любой серьезной статистической компьютерной программы и входит в основной инструментарий всех наук, имеющих дело с многопараметрическим описанием изучаемых объектов, таких, как социология, экономика, биология, медицина и другие.

Основная идея факторного анализа была сформулирована еще Ф. Гальтоном, основоположником измерений индивидуальных различий. Она сводится к тому, что если несколько признаков, измеренных на группе индивидов, изменяются согласованно, то можно предположить существование одной общей причины этой совместной изменчивости — фактора как скрытой (латентной), непосредственно не доступной измерению переменной. Далее К. Пирсон в 1901 году выдвигает идею «метода главных осей», а Ч. Спирмен, отстаивая свою однофакторную концепцию интеллекта, разрабатывает математический аппарат для оценки этого фактора, исходя из множества измерений способностей. В своей работе, опубликованной в 1904 году, Ч. Спирмен показал, что если ряд признаков попарно коррелируют друг с другом, _ то может быть составлена система линейных уравнений, связывающих все эти признаки, один общий фактор «общей одаренности» и по одному специфическому фактору «специальных способностей» для каждой переменной. В 1930-х годах Л. Терстоун впервые предлагает «многофакторный анализ» для описания многочисленных измеренных способностей меньшим числом общих факторов интеллекта, являющихся линейной комбинацией этих исходных способностей. С 1950-х годов, с появлением компьютеров, факторный анализ начинает очень широко использоваться в психологии при разработке тестов, обоснования структурных теорий интеллекта и личности. При этом исследователь начинает с множества измеренных эмпирических показателей, которые при помощи факторного анализа группируются по факторам (изучаемым свойствам). Факторы получают интерпретацию по входящим в них переменным, затем отбираются наиболее «весомые» показатели этих факторов, отсеиваются малозначимые переменные, вычисляются значения факторов для испытуемых и сопоставляются с внешними эмпирическими показателями изучаемых свойств.

В дальнейшем, по мере развития математического обеспечения факторного анализа, накопления опыта его использования, прежде всего в психологии, задача факторного анализа обобщается. Как общенаучный метод, факторный анализ становится средством для замены набора коррелирующих измерений существенно меньшим числом новых переменных (факторов). При этом основными требованиями являются: а) минимальная потеря информации, содержащейся в исходных данных, и б) возможность представления (интерпретации) факторов через исходные переменные.

Таким образом, главная цель факторного анализа — уменьшение размерности исходных данных с целью их экономного описания при условии минимальных потерь исходной информации. Результатом факторного анализа является переход от множества исходных переменных к существенно меньшему числу новых переменных — факторов. Фактор при этом интерпретируется как причина совместной изменчивости нескольких исходных переменных.

Если исходить из предположения о том, что корреляции могут быть объяснены влиянием скрытых причин — факторов, то основное назначение факторного анализа — анализ корреляций множества признаков.

ПРИМЕР 1

Рассмотрим результаты факторного анализа на простом примере. Предположим, исследователь измерил на выборке из 50 испытуемых 5 показателей интеллекта: счет в уме, продолжение числовых рядов, осведомленность, словарный запас, установление сходства. Все показатели статистически значимо взаимосвязаны на уровне р < 0,05, кроме показателя № 4 с № 1 и 2 (табл. 1).

Таблица 1 Матрица корреляций пяти показателей интеллекта

№	Показатели
	Счет в уме	1,00	0,88	0,33	0,23	0,42
	Числовые ряды	0,88	1,00	0,32	0,24	0,35
	Осведомленность	0,33	0,32	1,00	0,58	0,58
	Словарный запас	0,23	0,24	0,58	1,00	0,54
	Сходство	0,42	0,35	0,58	0,54	1,00

Таблица 2. Факторные нагрузки после варимакс-вращения

Исходные переменные	Факторные нагрузки	А2 (общность)
	Fy	Рг
	0,97	0,20	0,99
	0,86	0,20	0,78
	0,18	0,76	0,62
	0,09	0,74	0,56
	0,26	0,69	0,55
Собственное значение	1,79	1,70	3,5
Доля дисперсии	0,36	0,34	0,7

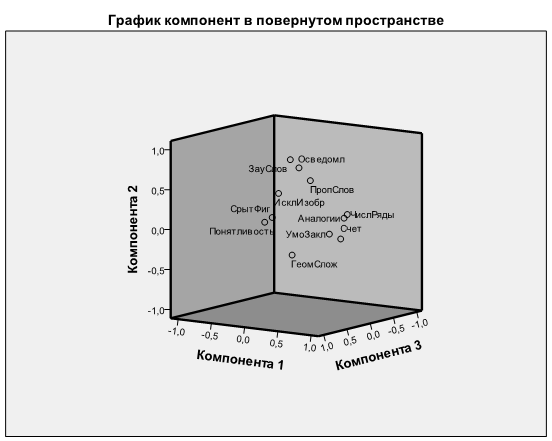
Применив факторный анализ, исследователь выделил два фактора. Основной результат, который подлежит интерпретации исследователем, — таблица факторных нагрузок после варимакс-вращения (табл. 2). Не рассматривая пока шаги, приводящие к этому результату, попытаемся проинтерпретировать полученные данные. В нашем примере по фактору 1 (F_{) максимальные нагрузки имеют переменные 1 и 2. Следовательно, фактор 1 и определяется этими переменными. Поскольку переменная 1 — счет в уме, а переменная 2 — продолжение числового ряда, то фактору 1 может быть присвоено название «арифметические способности», как показателю легкости оперирования числовым материалом. Точно так же фактору 2 можно присвоить название «вербальные способности», как показателю словесного понимания. Нетрудно заметить, что переменные, определяющие фактор, сильнее связаны друг с другом, чем с другими переменными (табл. 16.1). Так, переменные 1 и 2, определяющие фактор 1, сильнее связаны друг с другом, чем с переменными 3, 4 и 5. Таким образом, за взаимосвязью пяти исходных измерений способностей при помощи факторного анализа обнаруживается действие двух латентных переменных (факторов).

Интерпретация фактора через исходные переменные

Интерпретация факторов — одна из основных задач факторного анализа. Ее решение заключается в идентификации факторов через исходные переменные. Эта идентификация и осуществляется по результатам обработки, представленным в табл. 2.

Основное содержание табл. 2 — величины а_и... а₂$ — факторные нагрузки переменных 1... 5 (строки) по факторам 1 и 2 (столбцы). Факторные нагрузки — аналоги коэффициентов корреляции, показывают степень взаимосвязи соответствующих переменных и факторов: чем больше абсолютная величина факторной нагрузки, тем сильнее связь переменной с фактором, тем больше данная переменная обусловлена действием соответствующего фактора. Каждый фактор идентифицируется по тем переменным, с которыми он в наибольшей степени связан, то есть по переменным, имеющим по этому фактору наибольшие нагрузки. Идентификация фактора заключается, как правило, в присвоении ему имени, обобщающего по смыслу наименования входящих в него переменных.

Если исследователя интересует только структура измеренных признаков, на этом факторный анализ завершается. Продолжая факторный анализ, исследователь далее может вычислить значения факторов для испытуемых, например, с целью их дифференциации по преобладанию арифметических или вербальных способностей.

Выбирая факторный анализ как средство изучения корреляций, исследователь должен отдавать себе отчет в том, что это один из самых сложных и трудоемких методов. Зачастую нет веских оснований предполагать наличие факторов как скрытых причин изучаемых корреляции, и задача заключается лишь в обнаружении группировок тесно связанных переменных. Тогда целесообразнее вместо факторного анализа использовать кластерный анализ корреляций ( см. ниже ). Помимо простоты, кластерный анализ обладает еще одним преимуществом: его применение не связано с потерей исходной информации о связях между переменными, что неизбежно при факторном анализе. И уже после выделения групп тесно связанных переменных можно попытаться применить факторный анализ для их объяснения.

Итак, можно сформулировать основные задачи факторного анализа:

1. Исследование структуры взаимосвязей переменных. В этом случае каждая группировка переменных будет определяться фактором, по которому эти переменные имеют максимальные нагрузки.

2. Идентификация факторов как скрытых (латентных) переменных — причин взаимосвязи исходных переменных.

Вычисление значений факторов для испытуемых как новых, интегральных переменных. При этом число факторов существенно меньше числа исходных переменных. В этом смысле факторный анализ решает задачу сокращения количества признаков с минимальными потерями исходной информации.

Дата добавления: 2013-12-13