Кластерный анализ

Кластерный анализ решает задачу построения классификации, то есть разделения исходного множества объектов на группы (классы, кластеры). При этом предполагается, что у исследователя нет исходных допущений ни о составе классов, ни об их отличии друг от друга. Приступая к кластерному анализу, исследователь располагает лишь информацией о характеристиках (признаках) для объектов, позволяющей судить о сходстве (различии) объектов, либо только данными об их попарном сходстве (различии). В литературе часто встречаются синонимы кластерного анализа: автоматическая классификация, таксономический анализ, анализ образов (без обучения).

Несмотря на то, что кластерный анализ известен относительно давно (впервые изложен Тгуоп в 1939 году), распространение эта группа методов получила существенно позже, чем другие многомерные методы, такие, как факторный анализ. Лишь после публикации книги «Начала численной таксономии» биологами Р. Сокэл и П. Снит в 1963 году начинают появляться первые исследования с использованием этого метода. Тем не менее, до сих пор в психологии известны лишь единичные случаи удачного применения кластерного анализа, несмотря на его исключительную простоту. Вызывает удивление настойчивость, с которой психологи используют для решения простой задачи классификации (объектов, признаков) такой сложный метод, как факторный анализ. Вместе с тем, как будет показано в этой главе, кластерный анализ не только гораздо проще и нагляднее решает эту задачу, но и имеет несомненное преимущество: результат его применения не связан с потерей даже части исходной информации о различиях объектов или корреляции признаков.

Варианты кластерного анализа — это множество простых вычислительных процедур, используемых для классификации объектов. Классификация объектов — это группирование их в классы так, чтобы объекты в каждом классе были более похожи друг на друга, чем на объекты из других классов. Более точно, кластерный анализ — это процедура упорядочивания объектов в сравнительно однородные классы на основе попарного сравнения этих объектов по предварительно определенным и измеренным критериям.

Существует множество вариантов кластерного анализа, но наиболее широко используются методы, объединенные общим названием иерархический кластерный анализ (Hierarchical Cluster Analysis). В дальнейшем под кластерным анализом мы будем подразумевать именно эту группу методов. Рассмотрим основной принцип иерархического кластерного анализа на примере.

ПРИМЕР.1

Предположим, 10 студентам предложили оценить проведенное с ними занятие по двум критериям: увлекательность (Pref) и полезность (Use). Для оценки использовалась 10-балльная шкала. Полученные данные (2 переменные для 10 студентов) графически представлены в виде графика двумерного рассеивания (рис. 19.1). Конечно, классификация объектов по результатам измерения всего двух переменных не требует применения кластерного анализа: группировки и так можно выделить путем визуального анализа. Так, в данном случае наблюдаются четыре группировки: 9,2, Ъ — занятие полезное, но не увлекательное; 1, 10, 8 — занятие увлекательное, но бесполезное; 5, 7 — занятие и полезное и увлекательное; 4, 6 — занятие умеренно увлекательное и умеренно полезное. Даже для трех переменных можно обойтись и без кластерного анализа, так как компьютерные программы позволяют строить трехмерные графики. Но для 4 и более переменных визуальный анализданных практически невозможен. Тем не менее, общий принцип классификации объектов при помощи кластерного анализа не зависит от количества измеренных признаков, так как непосредственной информацией для этого метода являются различия между классифицируемыми объектами.

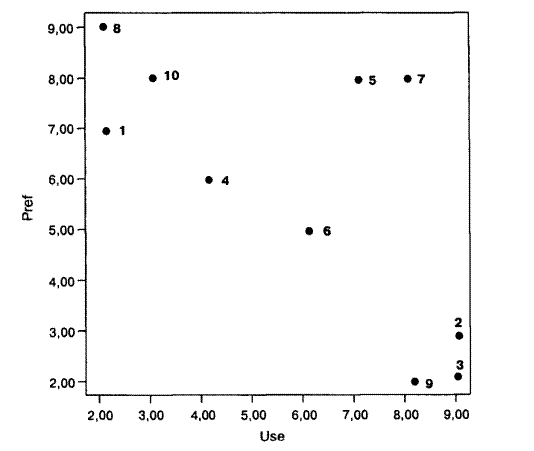Рис 1. Г рафик двумерного рассеивания переменных «увлекательность» (Pref) и «польза» (Use) для 10 студентов

Кластерный анализ объектов, для которых заданы значения количественных признаков начинается с расчета различий для всех пар объектов. Пользователь может выбрать по своему усмотрению меру различия. В качестве меры различия выбирается расстояние между объектами в Р-мерном пространстве признаков, чаще всего — евклидово расстояние или его квадрат. В данном случае Р= 2 и евклидово расстояние между объектами i и j определяется формулой:

где х — это значения одного, а у — другого признака.

На первом шаге кластерного анализа путем перебора всех пар объектов определяется пара (или пары) наиболее близких объектов, которые объединяются в первичные кластеры. Далее на каждом шаге к каждому первичному кластеру присоединяется объект (кластер), который к нему ближе. Этот процесс повторяется до тех пор, пока все объекты не будут объединены в один кластер. Критерий объединения объектов (кластеров) может быть разным и определяется методом кластерного анализа. Основным результатом применения иерархического кластерного анализа является дендрограмма — графическое изображение последовательности объединения объектов в кластеры. Для данного примера дендрограмма приведена на рис. 2

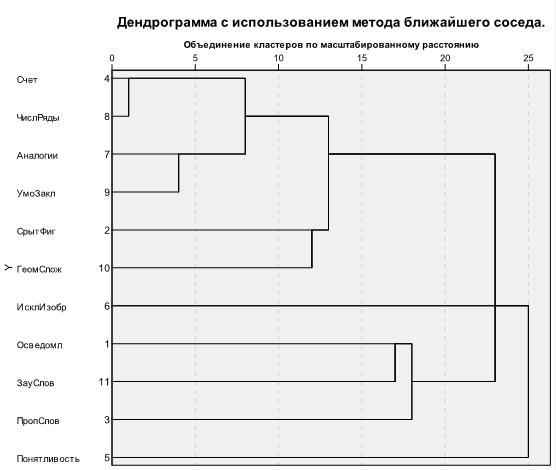
Рис. 19.2. Дендрограмма для 10 студентов (метод средней связи)

На дендрограмме номера объектов следуют по вертикали. По горизонтали отмечены расстояния (в условных единицах), на которых происходит объединение объектов в кластеры. На первых шагах происходит образование кластеров: (3,9,2) и (5,7). Далее образуется кластер (8, 10, 1) — расстояния между этими объектами больше, чем между теми, которые были объединены на предыдущих шагах. Следующий кластер — (4, 6). Далее в один кластер объединяются кластеры (5, 7) и (4, 6), и т. д. Процесс заканчивается объединением всех объектов в один кластер. Количество кластеров определяет по дендрограмме сам исследователь. Так, судя по дендрограмме, в данном случае можно выделить три или четыре кластера.

Как видно из примера, кластерный анализ — это комбинаторная процедура, имеющая простой и наглядный результат. Широта возможного применения кластерного анализа очевидна настолько же, насколько очевиден и его смысл. Классифицирование или разделение исходного множества объектов на различающиеся группы — всегда первый шаг в любой умственной деятельности, предваряющий поиск причин обнаруженных различий.

Можно указать ряд задач, при решении которых кластерный анализ является более эффективным, чем другие многомерные методы:

□ разбиение совокупности испытуемых на группы по измеренным признакам с целью дальнейшей проверки причин межгрупповых различий по внешним критериям, например, проверка гипотез о том, проявляются ли типологические различия между испытуемыми по измеренным признакам;

□ применение кластерного анализа как значительно более простого и наглядного аналога факторного анализа, когда ставится только задача группировки признаков на основе их корреляции;

□ классификация объектов на основе непосредственных оценок различий между ними (например, исследование социальной структуры коллектива по данным социометрии — по выявленным межличностным предпочтениям).

Несмотря на различие целей проведения кластерного анализа, можно выделить общую его последовательность как ряд относительно самостоятельных шагов, играющих существенную роль в прикладном исследовании:

1. Отбор объектов для кластеризации. Объектами могут быть, в зависимости от цели исследования: а) испытуемые; б) объекты, которые оцениваются испытуемыми; в) признаки, измеренные на выборке испытуемых.

2. Определение множества переменных, по которым будут различаться объекты кластеризации. Для испытуемых — это набор измеренных признаков, для оцениваемых объектов — субъекты оценки, для признаков — испытуемые. Если в качестве исходных данных предполагается использовать результаты попарного сравнения объектов, необходимо четко определить критерии этого сравнения испытуемыми (экспертами).

3. Определение меры различия между объектами кластеризации. Это первая проблема, которая является специфичной для методов анализа различий: многомерного шкалирования и кластерного анализа. Применяемые меры различия и требования к ним подробно изложены в главе 18 (раздел «Меры различия»),

4. Выбор и применение метода классификации для создания групп сходных объектов. Это вторая и центральная проблема кластерного анализа. Ее весомость связана с тем, что разные методы кластеризации порождают разные группировки для одних и тех же данных. Хотя анализ и заключается в обнаружении структуры, наделе в процессе кластеризации структура привносится в данные, и эта привнесенная структура может не совпадать с реальной.

5. Проверка достоверности разбиения на классы.

Последний этап не всегда необходим, например, при выявлении социальной структуры группы. Тем не менее следует помнить, что кластерный анализ всегда разобьет совокупность объектов на классы, независимо от того, существуют ли они на самом деле. Поэтому бесполезно доказывать существенность разбиения на классы, например, на основании достоверности различий между классами по признакам, включенным в анализ. Обычно проверяют устойчивость группировки — на повторной идентичной выборке объектов. Значимость разбиения проверяют по внешним критериям — признакам, не вошедшим в анализ.

Основная:

1. Сидоренко Е.В. Методы математической обработки в психологии. СПб, 2007.

2. Наследов А.Д. Математические методы психологического исследования. Анализ и интерпретация данных. СПб., Речь, 2006.

3. Наследов А.Д. SPSS компьютерный анализ данных в психологии и социальных науках. СПб., Питер. 2007.

4. Наследов А.Д. SPSS 19. Профессиональный статистический анализ данных. – Спб,: П. 2011. – 400 с.: ил.итер

5. Суходольский Г.В. Математическая психология. Харьков: Изд. Гуманитарный центр, 2006. – 306 с.

6. Ермолаев О.Ю. Математическая статистика для психологов. - М.: МПСИ, Флинта, 2003

ДОПОЛНИТЕЛЬНАЯ:

1.Артемьева Е.Ю., Мартынов Е.М. Вероятностные методы в психологии. - М Изд. МГУ, 1975.-206 с.

2. Басимов М.М. Изучение статистических связей в психологических исследованиях. Монография. М.: Издательство Московского психолого-социального института; Воронеж: НПО «МОДЭК», 2008. – 432 с.

3. Гласс Дж., Стенли Дж. Статистические методы в педагогике и психологии. М.: Прогресс, 1976. - 495 с.

4. Годфруа Ж. Что такое психология? М.: Мир, 1996.

5. Дюк В.А. Компьютерная психодиагоностика. Спб, 1994.

6. Рабочая книга социолога. - М.: Наука. 1983. - 477 с.

7. Как провести социологическое исследование. - М.: Политиздат, 1985.- 225.

8. Плис А.И., Сливина Н.А. Практикум по прикладной статистике в среде SPSS. М.: Финансы и статистика, 2004.

9. stat-msu.narod.ru - Учебные материалы по статистике для психологов. Учебные материалы по курсу математической статистики для психологического факультета МГУ. [электронный ресурс]

ОБРАЗОВАТЕЛЬНЫЕ ИНТЕРНЕТ РЕСУРСЫ

1. www.statsoft.ru (портал статистической обработки данных и электронный учебник по статистике в среде “Statistica 6.0”)

2. http://www.spss.ru/ (Сайт посвященный работе в среде SPSS, включая примеры и электронный учебник).

Перечень вопросов к зачету:

1. Шкалирование. Виды шкал.

2. Математическое ожидание случайной величины

3. Параметрические критерии различия.

4. Непараметрические критерии различия.

5. Математическое ожидание случайной величины.

6. Дисперсия случайной величины.

7. Двух модальное распределение случайной величины

8. Зависимые и независимые выборки. Стратифицированные выборки.

9. Репрезентативность и валидность выборки.

10. Гистограмма. Разброс выборки.

11. Нормальное распределение случайной величины.

12. Размах в пределах +/- 3 σ - стандартное отклонение от среднего для нормального распределения.

13. Понятие о статистических гипотезах. Нулевая и альтернативная гипотеза.

14. Понятие уровня статистической значимости. Мощность критерия.

15. Непараметрические критерии различия.

16. Критерий знаков (G- критерий) и критерий Вилкоксона. Типичный и нетипичный сдвиг.

17. Критерий Фридмана.

18. Критерий Манна-Уитни

19. Критерий Розенбаума.

20. Критерий Крускала – Уоллиса.

21. Параметрические критерии различий: t-критерий Стьюдента и его смысл.

22. Критерий Хи-квадрат и его смысл.

23. Корреляционный анализ: понятие корреляционной связи; коэффициент корреляции Пирсона.

24. Корреляционный анализ: ранговый коэффициент корреляции Спирмена.

25. Корреляционный анализ: коэффициент корреляции «τ» Кендала.

26. Кластерный анализ: основные идеи кластерного анализа.

27. Элементы факторного анализа. Вращение факторов. Основные задачи психологии, решаемые с использованием кластерного анализа.

Дата добавления: 2013-12-13