
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В.5. Элементарные функции
|
|
|
|
Функция называется явной, если она задана формулой вида y = f (x) (правая часть не содержит зависимой переменной).
Функция называется неявной, если она задана уравнением F (x, y) = 0, не разрешенным относительно зависимой переменной.
Пусть функция y = f (x) – функция от независимой переменной х с областью определения Х и областью значений Y. Поставим в соответствие  единственное значение
единственное значение  , при котором f (x) = y. Тогда полученная функция х = φ(у), определенная на промежутке Y с областью значений Х, называется обратной (обратную функцию также обозначают y = f -1(x)).
, при котором f (x) = y. Тогда полученная функция х = φ(у), определенная на промежутке Y с областью значений Х, называется обратной (обратную функцию также обозначают y = f -1(x)).
Для любой строго монотонной функции существует обратная функция. Графики взаимно обратных функций симметричны относительно прямой у = х (биссектрисы 1-го и 3-го координатных углов).
Пример 2. Для функции у = 3 х найти обратную.
Функция у = 3 х монотонная (возрастающая), следовательно, она имеет обратную. Для того чтобы получить формулу обратной функции выразим переменную х через у:
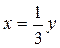 . А затем полученную формулу запишем в привычном виде (поменяем х и у местами): . А затем полученную формулу запишем в привычном виде (поменяем х и у местами):  - это и есть обратная функция к данной. - это и есть обратная функция к данной.
|
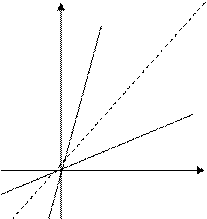 у у = х
у = 3 х у у = х
у = 3 х
 О х
О х
|
Пусть функция y = f (и) – функция переменной и определена на множестве U с областью значений Y, а переменная и – функция переменной х: и = φ(х), определена на множестве Х с областью значений U. Тогда заданная на множестве Х с областью значений Y функция y = f [φ(х)] называется сложной функцией (композицией функций, функцией от функции).
Например, у = cos(x 2+ x) – сложная функция, т.к. ее можно представить в виде, у = cos и, где и = x 2+ x.
Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Например, функция 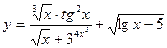 – элементарная (пример неэлементарной функции у = | x |).
– элементарная (пример неэлементарной функции у = | x |).
Классификация функций. Элементарные функции делятся на:
1) Алгебраические (полученные с помощью конечного числа алгебраических действий над аргументом). К ним относятся:
· целая рациональная функция (многочлен): 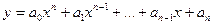 ;
;
· дробно-рациональная функция – отношение двух многочленов;
· иррациональная функция (в составе операций над аргументом есть извлечение корня).
2) Неалгебраические (или трансцендентные). К ним относятся: показательная, логарифмическая, тригонометрические, обратные тригонометрические.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 429; Нарушение авторских прав?; Мы поможем в написании вашей работы!