
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В. 7. Преобразование графиков
|
|
|
|
В.6. Интерполирование функций
Интерполирование – приближенное вычисление неизвестных значений функции по известным ее значениям в заданных точках.
Наиболее простым является линейное интерполирование, при котором допускается, что приращение функции пропорционально приращению аргумента.
Пример 3. Значение функции известно в точках a и b. С помощью линейной интерполяции найти значение функции в точке с.
| а | f(a) | b | f(b) | c |
| 2,42 | 2,04 | 2,88 | 2,008 |
Решение. Значение с лежит между а и b. Формула линейного интерполирования:
f(c)» f(a) + 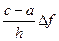 , где h = b – a, Df = f(b) – f(a).
, где h = b – a, Df = f(b) – f(a).
Подставляя в формулу известные значения из таблицы, получим:
f(2,008)» 2,42 + 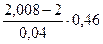 = 2,512. Ответ. f(2,008)» 2,512.
= 2,512. Ответ. f(2,008)» 2,512.
Пусть задан график функции y = f(x). Тогда справедливы следующие утверждения:
1. График функции y = f(x+a) есть график y = f(x), сдвинутый на | а | единиц параллельно оси Оy (вдоль оси Oх); при a > 0 – влево, при a < 0 – вправо.
2. График функции y = f(x)+b есть график y = f(x), сдвинутый | b | единиц параллельно оси Оx (вдоль оси Oy); при b > 0 – вверх, при b< 0 – вниз.
3. График функции y = mf(x) (m ≠0) есть график y = f(x), растянутый при m > 1 в m раз или сжатый при 0 < m <1 в m раз вдоль оси Oy. При m < 0 график функции y = mf(x) есть зеркальное отображение графика y = -mf(x) от оси Ox.
4. График функции y = f(kx) (k ≠0) есть график y = f(x), сжатый при k > 1 в k раз или растянутый при 0 < k < 1 в k раз вдоль оси Ox. При k < 0 график функции y = f(-kx) есть зеркальное отображение графика y = f(kx) от оси Oy.
5. График функции 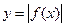 получается из графика функции y = f(x), если оставить на месте ту часть, где f(x) ≥ 0 и симметрично отобразить относительно Ох часть f(x) ˂ 0:
получается из графика функции y = f(x), если оставить на месте ту часть, где f(x) ≥ 0 и симметрично отобразить относительно Ох часть f(x) ˂ 0:
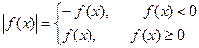 .
.
6. График функции 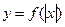 совпадает с графиком y = f(x) на множеств неотрицательных значений аргумента и симметричен ему относительно Оу на множестве отрицательных значений аргумента.
совпадает с графиком y = f(x) на множеств неотрицательных значений аргумента и симметричен ему относительно Оу на множестве отрицательных значений аргумента.
Пример 4. Построить график функции у = –4∙sin2 x + 1.
 Решение. 1) Сначала построим график функции у = sin x.
Решение. 1) Сначала построим график функции у = sin x.
у



 1
1



 О х
О х
 -π -
-π - -1
-1 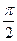 π
π
2) Сжатием графика в 2 раза вдоль оси Ох получаем график функции у =sin2 x.
 у
у
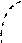
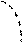
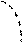
 1
1


 О х
О х
 -π -
-π -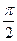
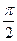 π
π
3) Растянем график у = sin2 x вдоль оси Оу в 4 раза и получим график функции
у = 4sin2 x.  у
у


 4
4
 |


 1
1




 О х
О х
 -π -
-π -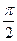
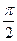 π
π
 |


-4
4) Зеркально отобразив график от оси Ох, получим у = –4sin2 x.
 у
у


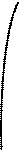
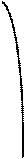
 4
4
 |


 1
1



 О х
О х
 -π -
-π -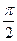
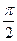 π
π
 |


-4
5) Сдвинем полученный график на 1 единицу вверх параллельно оси Оу. Таким образом график функции у = – 4∙sin2 x + 1 имеет вид:
 у
у


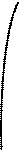
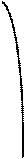
 5
5
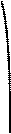
 |







 1
1

 π
π 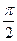 О
О 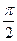 π х
π х
 |


-3
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 603; Нарушение авторских прав?; Мы поможем в написании вашей работы!