Исследование функции на выпуклость и точки перегиба

Функция y=ƒ(x) называется выпуклой вниз на промежутке X,если для "x₁,x₂ЄX

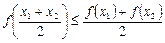
Функция y=ƒ(x) называется выпуклой вверх на промежутке X, если для "x₁,x₂ЄX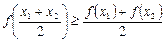

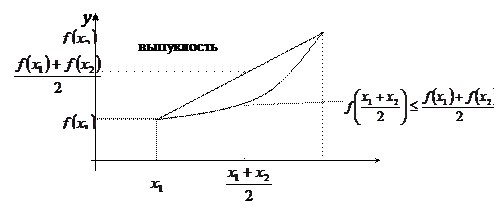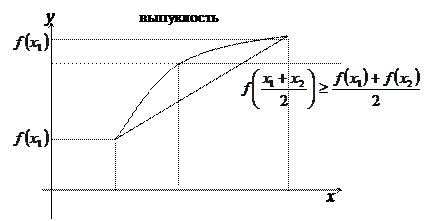
Теорема. Функция выпукла вниз (вверх) на промежутке X тогда и только тогда, когда её 1-ая производная на X монотонно возрастает (убывает).

Теорема. Если y=f(x) дважды дифференцируема а, f``(x)> 0 (f``(x)<0) внутри некоторого промежутка X, то функция выпукла вниз (вверх) на этом промежутке.

Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в которых функция выпукла вниз и вверх.

Отсюда следует, что точка перегиба – это точка экстремума 1- й производной.

Теорема (необходимое условие перегиба). В точке перегиба x₀ дважды дифференцируемой функции f```(x)=0.

Теорема.(достаточное условие перегиба). Если 2-я производная дважды дифференцируемой функции при переходе через точку x₀ меняет свой знак, то x₀ есть точка перегиба.

Замечание. Если критическая точка дифференцируемой функции не является точкой экстремума, то она есть точка перегиба.

Схема исследования функции на выпуклость и точки перегиба:

1. Найти f```(x).

2. Найти точки, в которых f```(x)=0 или не существует.

3. Исследовать знак 2-ой производной слева и справа от найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба.

4. Найти значения функции в точках перегиба.

Пример 7. Исследовать функцию 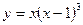на выпуклость и точки перегиба.

Дата добавления: 2013-12-13