Уравнение плоскости, проходящей через три точки

Различные виды задания плоскости

Общее уравнение плоскости.

ПЛОСКОСТЬ

Лекция 8

Дополнительная

1. Зайцев И.А, Высшая математика, М, Высшая школа, 1991, 400с,

2. Кудрявцев В.А., Демидович Б.П, Краткий курс высшей математики. М., Наука, 1984. 624с.

Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.

Определение. Плоскостью называется поверхность, вес точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0,

где А, В, С – координаты вектора 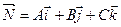-вектор нормали к плоскости.

Возможны следующие частные случаи:

А = 0 – плоскость параллельна оси Ох

В = 0 – плоскость параллельна оси Оу

С = 0 – плоскость параллельна оси Оz

D = 0 – плоскость проходит через начало координат

А = В = 0 – плоскость параллельна плоскости хОу

А = С = 0 – плоскость параллельна плоскости хОz

В = С = 0 – плоскость параллельна плоскости yOz

А = D = 0 – плоскость проходит через ось Ох

В = D = 0 – плоскость проходит через ось Оу

С = D = 0 – плоскость проходит через ось Oz

А = В = D = 0 – плоскость совпадает с плоскостью хОу

А = С = D = 0 – плоскость совпадает с плоскостью xOz

В = С = D = 0 – плоскость совпадает с плоскостью yOz

Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе координат.

Уравнение плоскости, проходящей через три точки:

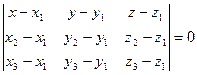
Дата добавления: 2013-12-13