Угол между двумя прямыми

Общее уравнение прямой, как линии пересечения двух плоскостей

Каноническое и общее уравнение прямой

ПРЯМАЯ В ПРОСТРАНСТВЕ

Пусть М ₁(x ₁, y ₁, z ₁) – точка, лежащая на прямой l, и 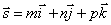– её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

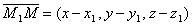Ясно, что векторы 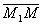и 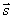коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

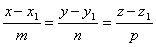– канонические уравнения прямой.

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

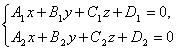
определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

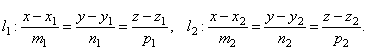
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и 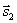. Так как 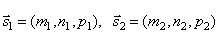, то по формуле для косинуса угла между векторами получим

.

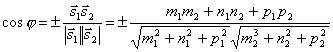Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов 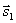и :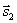

Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l ₁ параллельна l ₂ тогда и только тогда, когда 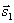параллелен .

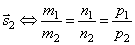Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю: .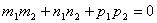

Дата добавления: 2013-12-13