Экстремум функции двух переменных

ЭКСТРЕМУМ ФУЕКЦИИ НЕСКОЛЬКИХ РЕМЕННЫХ

Лекция 11

Дополнительная

Основная

СПИСОК ЛИТЕРАТУРЫ

Вопросы для самоконтроля

Касательная плоскость и нормаль к поверхности.

Определение. Нормалью к поверхности в точке N₀ называется прямая, проходящая через точку N₀ перпендикулярно касательной плоскости к этой поверхности.

Если поверхность задана уравнением z = f(x, y), где f(x, y) – функция, дифференцируемая в точке М₀(х₀, у₀), то уравнение касательной плоскости в точке N₀(x₀,y_0,(x₀,y₀)) имеет вид:

.

Уравнение нормали к поверхности в этой точке:

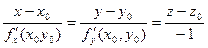
1. Что такое производная по направлению?

2. Что такое градиент?

3. Как находится касательная плоскость и нормаль к поверхности?

1. Дмитрий Письменный, Конспект лекций по высшей математике. М., АЙРИС ПРЕСС,2007.600с.

2. Данко П.Е., Попов Л.Г., Кожевникова Т.Е., Данко С.И. Высшая математика в упражнениях и задачах. 2006.-187с. ООО Изд. Мир и образование.

1. Зайцев И.А, Высшая математика, М, Высшая школа, 1991, 400с,

2. Кудрявцев В.А., Демидович Б.П, Краткий курс высшей математики. М., Наука, 1984. 624с.

.

Определение. Точка М₀(х₀, у₀) называется точкой максимума функции z = f(x, y), определенной в некоторой области D, если в некоторой окрестности точки М_0, принадлежащей области D, верно неравенство .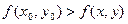

Определение. Точка М₀(х₀, у₀) называется точкой минимума функции z = f(x, y), определенной в некоторой области D, если в некоторой окрестности точки М_0, принадлежащей области D, верно неравенство .

Теорема. (Необходимые условия экстремума).

Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке обе частные производные первого порядка равны нулю , либо хотя бы одна из них не существует. Эта точка (х₀, у₀) называется критической (или стационарной) точкой.

Теорема. (Достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Пусть:

∆=AC-B²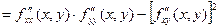. Тогда

1) Если ∆ (x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

А=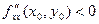- максимум, если - минимум.

2) Если ∆ (x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

3) Если ∆ (x₀, y₀) = 0, вывод о наличии экстремума сделать нельзя. Требуются дополнительные исследования.

11.2 Условный экстремум функции двух переменных.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f(x, y), не являются независимыми, т.е. существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи. Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Определение условного экстремума методом подстановки

u = f(x, y(x)).

В точках экстремума:

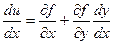=0 (1)

Определение условного экстремума методом Лагранжа

Выражение u = f(x, y) + lj(x, y) называется функцией Лагранжа.

В точках экстремума:

Выше мы рассмотрели функцию двух переменных, однако, все рассуждения относительно условного экстремума могут быть распространены на функции большего числа переменных.

Дата добавления: 2013-12-13