Формула Стокса.

Для поверхностных интегралов имеет место формула, позволяющая свести вычисление интеграла по поверхности σ к вычислению криволинейного интеграла по контуру L, ограничивающему эту поверхность.

Теорема Стокса. Если функции P(x, y, z), Q(x, y, z), R(x, y, z) непрерывны вместе со своими частными производными первого порядка, то имеет место формула

, (*)

где L - граница поверхности σ.

Направление криволинейного интеграла (вдоль L) и поверхностного (по σ) интегрирований согласованы между собой следующим правилом:

если человек, идущий по той

z 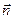σ стороне поверхности σ, по которой

производится поверхностное

L интегрирование, перемещается

вдоль границы L в направлении

криволинейного интегрирования,

то поверхность должна оставаться

слева.

0 y

D

x L₁

Формула (*) называется формулой Стокса.

Доказательство. Докажем теорему путем сведения поверхностного интеграла к двойному с последующим применением формулы Грина.

Будем считать, что поверхность σ пересекается с любой прямой, параллельной оси oz не более, чем в одной точке. Тогда уравнение этой поверхности будет z = z (x, y). Интегрирование будем вести по верхней стороне поверхности.

Рассмотрим интеграл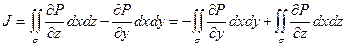

Из формулы определения поверхностного интеграла имеем

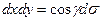
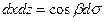
где γ и β – углы между нормалью 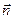и осями oz, oy

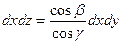
т.к. уравнение поверхности σ: z = z (x,y), то проекциями нормального вектора 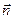будут , , 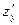-1, Направляющие косинусы пропорциональны этим проекциям, то 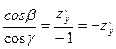поэтому .

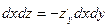Значит

Приведем этот интеграл к двойному. z заменим на z(x,y) и

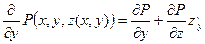
Таким образом, полагая , имеем ,

где D – проекция поверхности σ на плоскость xoy.

Применяя формулу Грина, получим

,

где L₁ – граница области D. Контур L₁ – есть проекция кривой L – границы поверхности σ на плоскость xoy.

Итак, 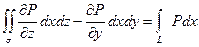(1)

Аналогично 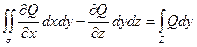(2)

(3)

Складывая почленно равенства (1), (2), (3) получим формулу Стокса.

Пример. Вычислить

,

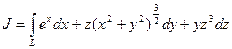где L – линия пересечения поверхностей

, , , ,

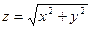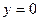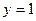
z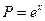

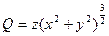
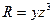
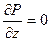
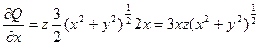
В

C

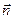
A

0 1 у

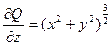
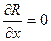
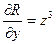
По формуле Стокса получим

Каждый из них сведем к двойному интегралу

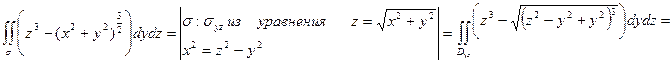
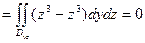
Окончательно J = -14.

Дата добавления: 2013-12-13