Нормальные системы линейных однородных дифференциальных уравнений с постоянными коэффициентами

При рассмотрении систем дифференциальных уравнений ограничимся случаем системы трех уравнений (n = 3). Все нижесказанное справедливо для систем произвольного порядка.

Определение. Нормальная система дифференциальных уравнений c постоянными коэффициентами называется линейной однородной, если ее можно записать в виде:

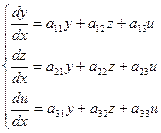(2)

Решения системы (2) обладают следующими свойствами:

1) Если y, z, u – решения системы, то Cy, Cz, Cu, где C = const – тоже являются решениями этой системы.

2) Если y₁, z₁, u₁ и y₂, z₂, u₂ – решения системы, то y₁ + y₂, z₁ + z₂, u₁ + u₂ – тоже являются решениями системы.

Решения системы ищутся в виде: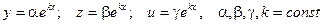

Подставляя эти значения в систему (2) и перенеся все члены в одну сторону и сократив на e^kx, получаем:

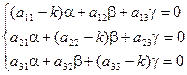
Для того, чтобы полученная система имела ненулевое решение необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.:

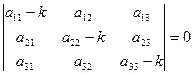
В результате вычисления определителя получаем уравнение третьей степени относительно k. Это уравнение называется характеристическим уравнением и имеет три корня k₁, k₂, k₃. Каждому из этих корней соответствует ненулевое решение системы (2):

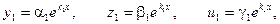
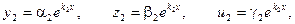
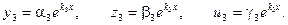
Линейная комбинация этих решений с произвольными коэффициентами будет решением системы (2):

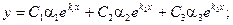
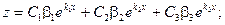
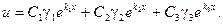
Пример. Найти общее решение системы уравнений:

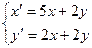
Составим характеристическое уравнение:

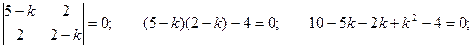
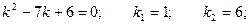
Решим систему уравнений:

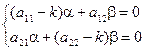
Для k₁:

Полагая 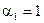(принимается любое значение), получаем: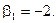

Для k₂: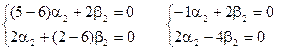

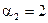Полагая (принимается любое значение), получаем: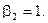

Общее решение системы: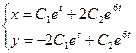

Этот пример может быть решен другим способом:

Продифференцируем первое уравнение: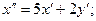

Подставим в это выражение производную у¢ = 2 x + 2 y из второго уравнения.

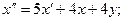
Подставим сюда у, выраженное из первого уравнения:

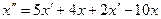
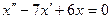
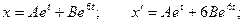
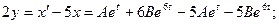
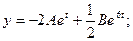
Обозначив 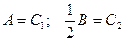, получаем решение системы: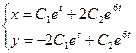

Пример. Найти решение системы уравнений

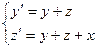
Эта система дифференциальных уравнений не относится к рассмотренному выше типу, т.к. не является однородным (в уравнение входит независимая переменная х).

Для решения продифференцируем первое уравнение по х. Получаем:

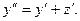
Заменяя значение z’ из второго уравнения получаем: .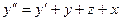

С учетом первого уравнения, получаем: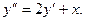

Решаем полученное дифференциальное уравнение второго порядка.

Общее решение однородного уравнения: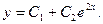

Теперь находим частное решение неоднородного дифференциального уравнения по формуле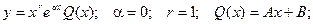

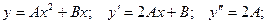
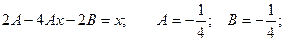
Общее решение неоднородного уравнения:

Подставив полученное значение в первое уравнение системы, получаем:

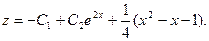
Пример. Найти решение системы уравнений:

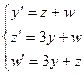
Составим характеристическое уравнение:

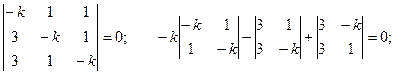
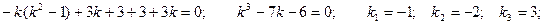
1) k = -1.

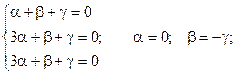
Если принять g = 1, то решения в этом случае получаем:

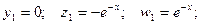
2) k₂ = -2.

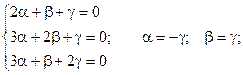
Если принять g = 1, то получаем:

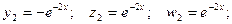
3) k₃ = 3.

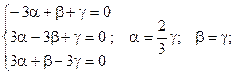
Если принять g = 3, то получаем:

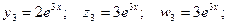
Общее решение имеет вид:

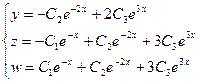
Дата добавления: 2013-12-13