
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Дифференцируемость функции в точке и на промежутке
|
|
|
|
Лекция 23. Понятие производной и её смысл (геометрический, физический, экономический). Производные элементарных функций. (Вывод). Таблица производных. Правила дифференцирования. Дифференциал и его смысл.
Таблица эквивалентных бесконечно малых
Лекция 22. Замечательные пределы. Первый и второй замечательные пределы. Таблица эквивалентных бесконечно малых.
Вычислению многих пределов, содержащих неопределенности, часто помогает использование двух так называемых замечательных пределов:
1) 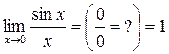 (x – угол в радианах)
(x – угол в радианах)
(1)
2) 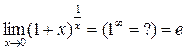 , где
, где  .
.
(в другом виде 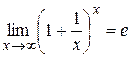 )
)
Докажем первый замечательный предел. Для этого вспомним школьную формулу для длины l произвольной дуги окружности (рис.1):
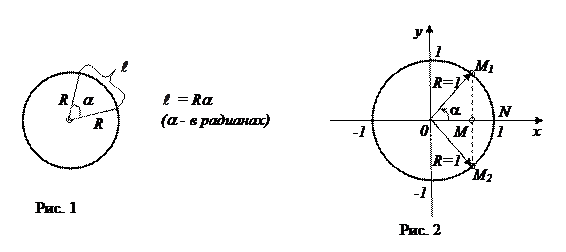
А теперь рассмотрим рис. 2:
 ;
;  ;
; 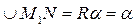 ;
;  ;
; 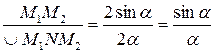 (
( – в радианах).
– в радианах).
При 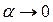 хорда M 1 M 2 и дуга M 1 NM 2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при
хорда M 1 M 2 и дуга M 1 NM 2, неограниченно уменьшаясь, практически становятся неразличимыми (малая дуга практически не отличается от стягивающей ее хорды). То есть их отношение стремится к единице. Таким образом, при 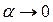 дробь
дробь  . А это и означает, что
. А это и означает, что
 (
( – угол в радианах)
– угол в радианах)
Полученный результат совпадает (при другом обозначении) с первым замечательным пределом (1).
Второй замечательный предел, приводит к важному для всей высшей математики числу e (к Неперову числу – по имени шотландского математика 16–го века Джона Непера, введшего в математику это число). Приведем доказательство.
Теорема 1: Переменная величина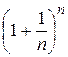 , где n - натуральное число, при
, где n - натуральное число, при  имеет предел, заключенный между 2 и 3.
имеет предел, заключенный между 2 и 3.
Доказательство: По формуле бинома Ньютона мы можем написать:

Произведем алгебраические преобразования.
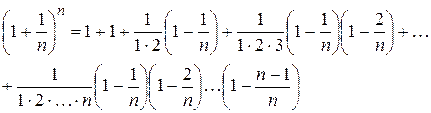 (2)
(2)
Из полученного равенства можно сделать вывод, что переменная величина 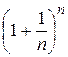 является возрастающей. Действительно,
является возрастающей. Действительно,
1) все члены разложения – положительны;
2) при переходе от значения n к (n+1) каждое слагаемое суммы возрастает, т.к. 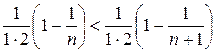 ;
;
3) добавляется ещё одно слагаемое.
Также переменная величина 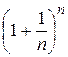 ограничена. Докажем этот факт. Учитывая, что
ограничена. Докажем этот факт. Учитывая, что  ;
;  и т.д., из (2) получаем
и т.д., из (2) получаем 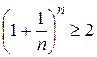 и
и
 .
.
Заметив, что  . Используем эти оценки и получим:
. Используем эти оценки и получим: 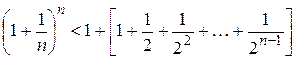 . Слагаемые в квадратных скобках образуют геометрическую прогрессию со знаменателем
. Слагаемые в квадратных скобках образуют геометрическую прогрессию со знаменателем  и первым членом
и первым членом  . Поэтому
. Поэтому 
 . Подытоживая все сказанное, получаем:
. Подытоживая все сказанное, получаем:  .
.
Итак, переменная величина 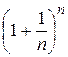 - возрастающая и ограниченная. На основании свойств пределов она имеет предел. Этот предел обозначим буквой е.
- возрастающая и ограниченная. На основании свойств пределов она имеет предел. Этот предел обозначим буквой е.
Теорема 2: Функция 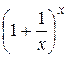 при
при  стремится к числу е.
стремится к числу е.
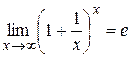 .
.
Доказательство: по теореме 1  , если n принимает целые положительные значения. Пусть теперь x стремится к бесконечности, принимая как дробные, так и отрицательные значения.
, если n принимает целые положительные значения. Пусть теперь x стремится к бесконечности, принимая как дробные, так и отрицательные значения.
1) Пусть 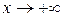 . Каждое его значение заключено между двумя положительными целыми числами
. Каждое его значение заключено между двумя положительными целыми числами  . При этом будут выполняться неравенства:
. При этом будут выполняться неравенства:

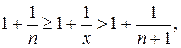
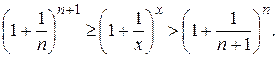
Если  , то
, то  . Найдем пределы переменных величин, между которыми заключена функция
. Найдем пределы переменных величин, между которыми заключена функция 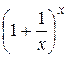 .
.
 .
.
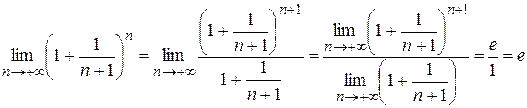 .
.
Следовательно, по свойствам пределов мы имеем 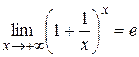 .
.
2) Пусть 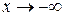 . Введем новую переменную t=-(x+1) или x=-(t+1). При
. Введем новую переменную t=-(x+1) или x=-(t+1). При 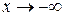 новая переменная
новая переменная  . Сделаем замену переменной и получим:
. Сделаем замену переменной и получим:

Что и требовалось доказать.
Число 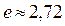 , как и число
, как и число  , принадлежит к числу важнейших математических констант. А такие функции, как
, принадлежит к числу важнейших математических констант. А такие функции, как  и
и  , принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция
, принадлежат к числу важнейших элементарных функций, используемых в высшей математике. Графики этих функций показаны на рисунках (3.12) и (3.13). При этом показательная функция  называется экспоненциальной, а ее график называется экспонентой. А логарифмическая функция
называется экспоненциальной, а ее график называется экспонентой. А логарифмическая функция  называется функцией натурального логарифма, а ее график называется натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию e назвали натуральным – от слова «natur» (природа).
называется функцией натурального логарифма, а ее график называется натуральной логарифмической кривой. Эти функции играют большую роль при математическом описании различного рода природных процессов. Именно поэтому, в частности, логарифм по основанию e назвали натуральным – от слова «natur» (природа).

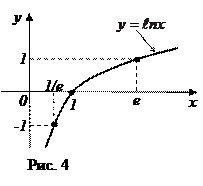
В математических справочниках имеются таблицы этих двух важных функций - и  , и
, и 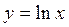 . Впрочем, для вычисления натуральных логарифмов
. Впрочем, для вычисления натуральных логарифмов 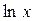 можно воспользоваться и таблицами общеизвестных десятичных логарифмов
можно воспользоваться и таблицами общеизвестных десятичных логарифмов  , если применить формулу перехода в логарифмах от одного основания к другому:
, если применить формулу перехода в логарифмах от одного основания к другому:
 ;
;
 (2.8)
(2.8)
При использовании замечательных пределов имеют в виду следующее обстоятельство: значение предела зависит от вида функции и того, к какому пределу стремится переменная, но не зависит от обозначения переменной.
Пример 1.  .
.
Пример 2.  ;
;
(при преобразованиях использовано обозначение  ).
).
Пример 3.  ;
;
(при преобразованиях использовано обозначение  ).
).
Пример 4.  .
.
Пример 5.  .
.
Пример 6. Найти 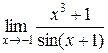 .
.
Используя формулу суммы кубов, преобразуем выражение под знаком предела: 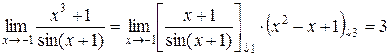 .
.
Пример 7. Найти  .
.
Решение.

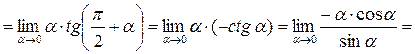
 .
.
Пример 8. Найти  .
.
Решение. 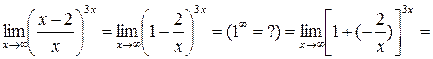
=| введем обозначение:  (
( ); тогда
); тогда  ;
;  |=
|=
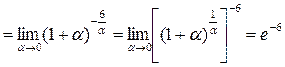 .
.
Пример 9: Найти  .
.
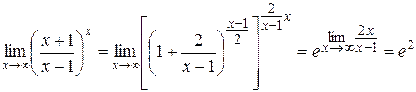
Пример 10: Найти 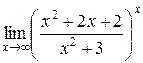 .
.

Пример 11: Найти 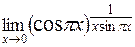 .
.
Чтобы подогнать структуру этого предела под структуру второго замечательного предела в основании степени прибавим и вычтем 1.

Выведем формулу, удобную для нахождения пределов в случае применения второго замечательного предела (неопределенности вида 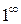 ). Пусть
). Пусть  . Здесь a может быть любым конечным числом или
. Здесь a может быть любым конечным числом или 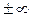 . Рассмотрим предел степени этих функций:
. Рассмотрим предел степени этих функций:

Итак, 
Пример 12. Найти 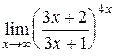 .
.
Проверим: 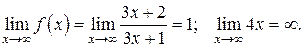
Найдем 
Тогда 
Пример 13. 
Пример 14. 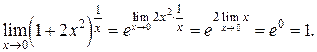
Пример 15. 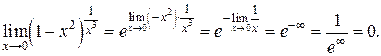
Для самостоятельного решения:
1. Найти  . Ответ:
. Ответ: 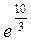 .
.
2. Найти  . Ответ:
. Ответ:  .
.
3. Найти 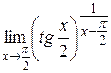 . Ответ: е.
. Ответ: е.
4. Найти  . Ответ:
. Ответ: 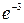 .
.
5. Найти  . Ответ: -4/5.
. Ответ: -4/5.
6. Найти  . Ответ:
. Ответ:  .
.
7. Найти 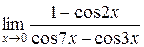 . Ответ: -1/10.
. Ответ: -1/10.
Кроме уже упомянутых первого и второго замечательных пределов, существует целый список пределов аналогичных ему по структуре и использованию:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 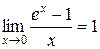 ;
;
8)  ;
;
9)  ;
;
10)  .
.
11)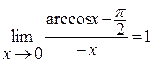 .
.
К этому списку полезно помнить следующие тригонометрические тождества: 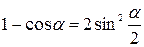 ;
;  .
.
Принцип использования этого списка очень прост: нужно подогнать структуру в искомом пределе под структуру соответствующего выражения в табличном пределе. Все необходимые сомножители либо выделяются из имеющегося выражения, либо приобретаются путем умножения и деления на него, либо выделяются с помощью преобразований исходного выражения. Приведем доказательство некоторых пределов из этого списка.
а) 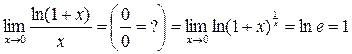 – согласно (2.7);
– согласно (2.7);
б)  ;
;
в) 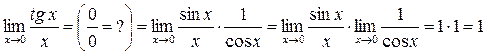 ;
;
г) 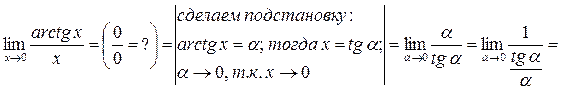
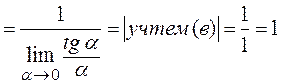 ;
;
д) 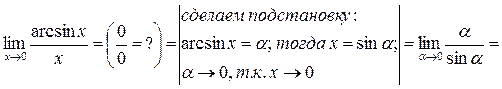
 ;
;
е) 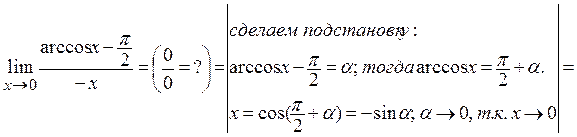
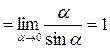 .
.
Часто перед тем, как применить табличные пределы, нужно провести какие-либо дополнительные, уже описанные ранее, стандартные преобразования или сделать замену переменной. Рассмотрим пример, в котором нужно избавиться от иррациональности.
Пример 16 Найти  .
.
Для того, чтобы избавиться от иррациональности в знаменателе, нужно умножить числитель и знаменатель на 

Другое стандартное преобразование «плюс-минус единица» встречается на практике в примерах, содержащих логарифмы и степенные функции. В этих случаях логарифмируемое выражение и основание степенной функции при 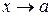 действительно стремится к 1, но они задаются в таком виде, где постоянное слагаемое 1 отсутствует. Чтобы пользоваться табличными пределами, нужно преобразовать логарифмируемое выражение и основание степени к требуемому виду. Для этого и используется стандартное преобразование «плюс-минус единица». При этом мы явно получаем 1 и выражение
действительно стремится к 1, но они задаются в таком виде, где постоянное слагаемое 1 отсутствует. Чтобы пользоваться табличными пределами, нужно преобразовать логарифмируемое выражение и основание степени к требуемому виду. Для этого и используется стандартное преобразование «плюс-минус единица». При этом мы явно получаем 1 и выражение  , что позволит далее использовать табличные пределы.
, что позволит далее использовать табличные пределы.
Пример 17: Найти  .
.

Пример 18:Найти  .
.
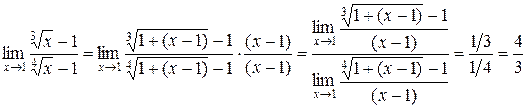 .
.
Если под знаком предела делается замена переменной, то все величины, входящие под знак предела, должны быть выражены через эту новую переменную, и из равенства, выражающего зависимость между старой переменной и новой, должен быть определен предел новой переменной. Рассмотрим пример, в котором наиболее целесообразным представляется замена переменной.
Пример 19: Найти  .
.
При  не существует предела
не существует предела 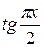 . Сделаем подстановку:
. Сделаем подстановку:  . Когда
. Когда  , то новая переменная
, то новая переменная 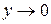 , так как
, так как 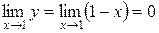 . Если
. Если  , то
, то  ; выражение, стоящее под знаком предела перепишется так:
; выражение, стоящее под знаком предела перепишется так: 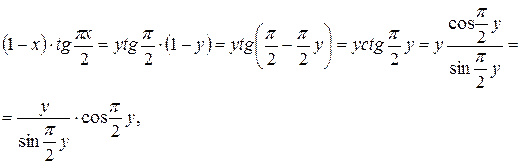
поэтому 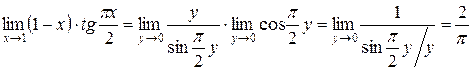
Табличные пределы можно использовать для вычисления других пределов при раскрытии неопределенностей вида 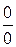 , заменяя одни функции на им эквивалентные бесконечно малые. Функции
, заменяя одни функции на им эквивалентные бесконечно малые. Функции  называются эквивалентными бесконечно малыми при
называются эквивалентными бесконечно малыми при 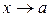 , если
, если 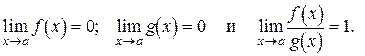 Другими словами эквивалентность означает выполнение предельного равенства. Эквивалентность двух функций обозначается волнистой чертой:
Другими словами эквивалентность означает выполнение предельного равенства. Эквивалентность двух функций обозначается волнистой чертой:  .
.
При раскрытии неопределенности функцию или функции, входящие в предел, можно заменить на им эквивалентные:


Замена во втором случае возможна, если 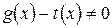 . Используя замечательные пределы, можно составить таблицу эквивалентных бесконечно малых.
. Используя замечательные пределы, можно составить таблицу эквивалентных бесконечно малых.
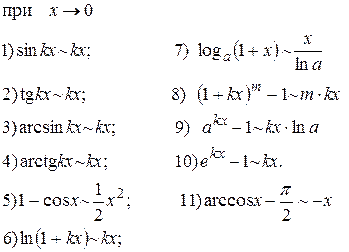 (3)
(3)
Приведем несколько примеров использования эквивалентных функций при вычислении пределов.
Пример 20.
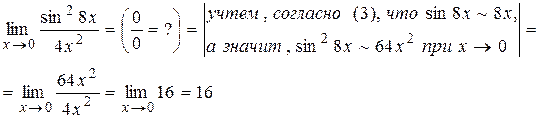
Пример 21.

Пример 22.
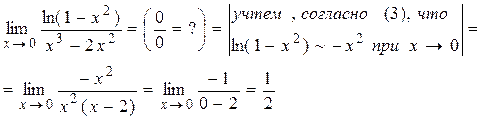
Пример 23. 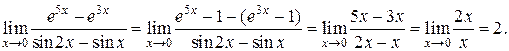
Пример 24.
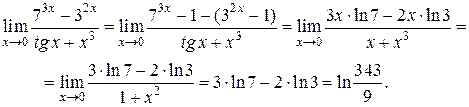
Пример 25.
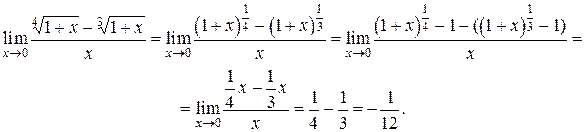
Пример 26. 
Для самостоятельного решения:
1. Найти  . (1/2).
. (1/2).
2. Найти  . (
. ( ).
).
3. Найти  . (
. (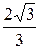 ).
).
4. Найти  . (1/е).
. (1/е).
5. Найти  . (1/2).
. (1/2).
6. Найти  . (1).
. (1).
7. Найти  . (1).
. (1).
8. Найти 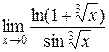 . (1).
. (1).

Дифференциальное исчисление – это раздел высшей математики, базирующийся на использовании таких ключевых для всей высшей математики понятий, как производные и дифференциалы функций. Эти понятия были введены в математику в конце 17 века Исааком Ньютоном и Готфридом Лейбницем.
Производная функции рассматривалась в школьном курсе математики. Поэтому сначала кратко повторим пройденное.
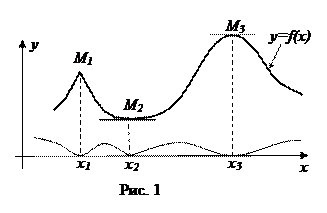 Пусть
Пусть  – некоторая непрерывная функция (ее график – сплошная линия) – рис..1. Здесь (М 1, М 2, М 3,…) – вершины и впадины графика функции. А их проекции (x 1, x 2, x 3,…) на ось ох называются соответственно точками максимума и минимума функции. Эти точки имеют и общее название: точки экстремума функции. Повторим еще раз: точки экстремума (точки максимума и минимума) функции – это не вершины и впадины графика функции, а их проекции на ось ох.
– некоторая непрерывная функция (ее график – сплошная линия) – рис..1. Здесь (М 1, М 2, М 3,…) – вершины и впадины графика функции. А их проекции (x 1, x 2, x 3,…) на ось ох называются соответственно точками максимума и минимума функции. Эти точки имеют и общее название: точки экстремума функции. Повторим еще раз: точки экстремума (точки максимума и минимума) функции – это не вершины и впадины графика функции, а их проекции на ось ох.
Интервал оси ох, на котором с увеличением аргумента x растет и функция y, называется интервалом возрастания функции. А интервал оси ох, на котором с увеличением аргумента x функция y убывает, называется интервалом ее убывания. В частности, на рис. 1 интервалы (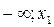 ) и (x 2; x 3) – интервалы возрастания функции
) и (x 2; x 3) – интервалы возрастания функции  , а интервалы (x1; x2) и (
, а интервалы (x1; x2) и ( ) – интервалы ее убывания.
) – интервалы ее убывания.
Функция, возрастающая (убывающая) на некотором интервале, считается возрастающей (убывающей) в каждой точке x этого интервала.
Заметим, что возрастая или убывая на интервале, функция делает это для разных x, вообще говоря, неодинаково быстро. Например, возрастающая на интервале (x 2; x 3) функция  (рис..1) сначала для x, близких к x 2, растет медленно (график функции поднимается медленно); затем, по мере увеличения x, крутизна подъема графика функции возрастает, а значит, увеличивается и скорость роста функции; затем, по мере приближения x к x 3, скорость роста функции снижается. В точке x 3 рост функции прекращается и затем, для
(рис..1) сначала для x, близких к x 2, растет медленно (график функции поднимается медленно); затем, по мере увеличения x, крутизна подъема графика функции возрастает, а значит, увеличивается и скорость роста функции; затем, по мере приближения x к x 3, скорость роста функции снижается. В точке x 3 рост функции прекращается и затем, для  , начинается убывание функции. И оно тоже, очевидно, происходит для разных x с разной скоростью.
, начинается убывание функции. И оно тоже, очевидно, происходит для разных x с разной скоростью.
Возникает естественная задача: оценить скорость изменения функции (скорость ее роста или убывания) в каждой точке x численно. Эта задача решена в конце 17 века Ньютоном и Лейбницем путем введения в математику понятия производной функции.
 Вспомним, как вводится это понятие. Пусть
Вспомним, как вводится это понятие. Пусть  – некоторая непрерывная на интервале (a; b) оси ох функция. Если на этом интервале взять конкретное значение аргумента x (конкретную точку x), то в этой точке функция y получит конкретное значение
– некоторая непрерывная на интервале (a; b) оси ох функция. Если на этом интервале взять конкретное значение аргумента x (конкретную точку x), то в этой точке функция y получит конкретное значение  . А теперь изменим x на некоторое
. А теперь изменим x на некоторое  , то есть перейдем от x к
, то есть перейдем от x к  (
(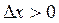 или
или 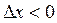 ), причем возьмем
), причем возьмем  такое, чтобы и точка
такое, чтобы и точка  тоже принадлежала интервалу (a; b) (рис.2).
тоже принадлежала интервалу (a; b) (рис.2).
Переход от x к  означает, что аргумент x получил приращение (изменение)
означает, что аргумент x получил приращение (изменение)  . При этом, естественно, и функция
. При этом, естественно, и функция  получит некоторое изменение (приращение)
получит некоторое изменение (приращение)  :
:
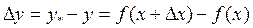 (1)
(1)
Приращение функции  , как и приращение аргумента
, как и приращение аргумента  , может быть любого знака – как положительным, так и отрицательным.
, может быть любого знака – как положительным, так и отрицательным.
А теперь рассмотрим отношение  , то есть отношение приращения функции к приращению аргумента. Это отношение показывает, на сколько единиц в среднем изменится y, если x изменится на единицу длины участка
, то есть отношение приращения функции к приращению аргумента. Это отношение показывает, на сколько единиц в среднем изменится y, если x изменится на единицу длины участка 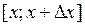 . То есть отношение
. То есть отношение  определяет среднюю скорость изменения функции
определяет среднюю скорость изменения функции  на участке
на участке 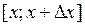 оси ох.
оси ох.
Проиллюстрируем оправданность этого термина «средняя скорость» на механическом примере. Пусть функция  определяет закон движения некоторой материальной точки по траектории ее движения, где x – время, а y – координата точки на траектории (рис. 3). Как и на реальной дороге, координату y точки на траектории ее движения можно понимать как удаленность этой точки от некоторой начальной точки О (от города, например). Зная закон движения
определяет закон движения некоторой материальной точки по траектории ее движения, где x – время, а y – координата точки на траектории (рис. 3). Как и на реальной дороге, координату y точки на траектории ее движения можно понимать как удаленность этой точки от некоторой начальной точки О (от города, например). Зная закон движения  движущейся точки, мы можем определить координату y этой точки в любой интересующий нас момент времени x. Тогда за время
движущейся точки, мы можем определить координату y этой точки в любой интересующий нас момент времени x. Тогда за время  , прошедшее с момента x до момента
, прошедшее с момента x до момента  , координата y движущейся точки изменится со значения
, координата y движущейся точки изменится со значения  до значения
до значения  , то есть точка получит перемещение
, то есть точка получит перемещение  , определяемое формулой (1). Заметим, что это перемещение может быть и положительным, и отрицательным. Положительным оно будет, если точка удаляется от начальной точки О (у нее тогда будет расти y), а отрицательным – если точка приближается к точке О (у нее тогда y будет убывать). При этом средняя скорость движения за время
, определяемое формулой (1). Заметим, что это перемещение может быть и положительным, и отрицательным. Положительным оно будет, если точка удаляется от начальной точки О (у нее тогда будет расти y), а отрицательным – если точка приближается к точке О (у нее тогда y будет убывать). При этом средняя скорость движения за время  (с момента x до момента
(с момента x до момента  ) будет равна
) будет равна
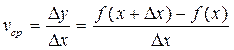 (2)
(2)
Одновременно отношение (2) является и средней скоростью изменения функции  на участке
на участке 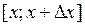 .
.
Однако нас в конечном итоге интересует не средняя скорость изменения функции на участке, а истинная (мгновенная) скорость её изменения в заданной точке x. В частности, нас интересует мгновенная скорость движения точки по ее траектории (скорость в заданный момент времени x).
Чтобы получить эту скорость, нужно, очевидно, стянуть промежуток 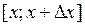 в точку x, то есть устремить
в точку x, то есть устремить  к нулю. При этом, в силу непрерывности функции
к нулю. При этом, в силу непрерывности функции  , и
, и  устремится к нулю, а отношение
устремится к нулю, а отношение  устремится к искомой мгновенной скорости изменения функции
устремится к искомой мгновенной скорости изменения функции  в точке х. То есть мгновенная скорость
в точке х. То есть мгновенная скорость  изменения функции
изменения функции  в точке х - это
в точке х - это
 (3)
(3)
В частности,  - это мгновенная скорость движения точки по ее траектории в момент времени х, если
- это мгновенная скорость движения точки по ее траектории в момент времени х, если  - закон движения точки.
- закон движения точки.
Определение. Предел (3), представляющий собой мгновенную скорость изменения функции  в точке х, называется производной функции
в точке х, называется производной функции  в точке x. Используется несколько различных стандартных обозначений этой производной:
в точке x. Используется несколько различных стандартных обозначений этой производной:
 (4)
(4)
Последнее из этих обозначений использовал Ньютон, предпоследнее - Лейбниц, а первые три ввел французский математик Коши. В дальнейшем мы в основном для обозначения производной функции  будем использовать обозначение Коши
будем использовать обозначение Коши  (или
(или 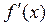 ), а при необходимости и
), а при необходимости и  (читается: производная функции y по переменной x).
(читается: производная функции y по переменной x).
Итак,
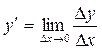 , (5)
, (5)
или подробнее
 (6)
(6)
– математическое определение производной функции  в заданной точке x. Читается это определение так: производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
в заданной точке x. Читается это определение так: производная функции – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Если x – время, а y – координата движущейся точки на траектории ее движения (рис. 3), то функция  определяет закон движения точки, а производная этой функции – мгновенную скорость движения точки по ее траектории:
определяет закон движения точки, а производная этой функции – мгновенную скорость движения точки по ее траектории:
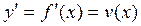 (7)
(7)
В этом состоит физический смысл производной функции.
 Но у производной функции есть и наглядный геометрический смысл. Для его выяснения рассмотрим рис. 4. Проведем к графику функции
Но у производной функции есть и наглядный геометрический смысл. Для его выяснения рассмотрим рис. 4. Проведем к графику функции  через точку
через точку  и точку
и точку  секущую
секущую  , а через точку
, а через точку  касательную L. Их углы наклона к оси ох обозначим соответственно
касательную L. Их углы наклона к оси ох обозначим соответственно  и
и 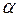 . Из
. Из  следует:
следует:
 (8)
(8)
Если устремить  к нулю, то и
к нулю, то и  устремится к нулю, а точка N устремится к точке M. Соответственно секущая
устремится к нулю, а точка N устремится к точке M. Соответственно секущая  устремится к касательной L, проведенной в точке M, а угол наклона
устремится к касательной L, проведенной в точке M, а угол наклона  секущей устремится к углу наклона
секущей устремится к углу наклона 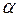 касательной. То есть
касательной. То есть  при
при 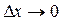 . Но тогда
. Но тогда
 при
при 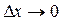 (9)
(9)
Иначе говоря,
 , (10)
, (10)
что с учетом (5) дает
 (11)
(11)
То есть производная функции  в точке x – это угловой коэффициент касательной, проведенной к графику функции в точке графика с абсциссой x (см. рис. 5).
в точке x – это угловой коэффициент касательной, проведенной к графику функции в точке графика с абсциссой x (см. рис. 5).  В этом и состоит геометрический смысл производной функции.
В этом и состоит геометрический смысл производной функции.
Производной функции можно придать и наглядный экономический смысл, причем разносторонний.
1. Пусть, например,  – количество произведенной продукции за время t. Тогда за время
– количество произведенной продукции за время t. Тогда за время  , прошедшее с момента t до момента
, прошедшее с момента t до момента  , будет произведено
, будет произведено  единиц продукции. При этом отношение
единиц продукции. При этом отношение  – это, очевидно, средняя производительность труда на промежутке времени
– это, очевидно, средняя производительность труда на промежутке времени  длительностью
длительностью  . Она выражает среднее количество продукции, произведенной за единицу времени этого промежутка. А тогда предел
. Она выражает среднее количество продукции, произведенной за единицу времени этого промежутка. А тогда предел
 (12)
(12)
– это так называемая предельная (истинная) производительность труда в момент времени t.
2. Пусть x – количество выпускаемой продукции (в некоторых единицах), а y – соответствующие издержки на ее производство (в рублях). То есть y – себестоимость продукции x. Тогда  – зависимость себестоимости продукции y от ее объема x.
– зависимость себестоимости продукции y от ее объема x.
Если объем продукции вырастет с x до  , то есть вырастет на
, то есть вырастет на  единиц, то ее себестоимость вырастет на
единиц, то ее себестоимость вырастет на 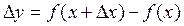 рублей. Тогда
рублей. Тогда  – средняя себестоимость продукции, приходящаяся на единицу ее прироста. А
– средняя себестоимость продукции, приходящаяся на единицу ее прироста. А
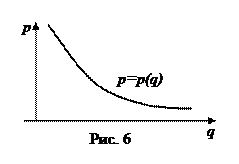
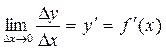 (13)
(13)
– так называемая предельная себестоимость продукции, определяющая затраты на производство единицы дополнительной продукции, если достигнутый объем производства составляет x единиц.
3. Пусть 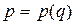 – так называемая кривая спроса, определяющая связь между ценой p единицы товара и спросом q на этот товар (q – количество товара, который может быть продан при цене p за его единицу) – рис. 6.
– так называемая кривая спроса, определяющая связь между ценой p единицы товара и спросом q на этот товар (q – количество товара, который может быть продан при цене p за его единицу) – рис. 6.
Кривая спроса, естественно, является убывающей кривой. Ее форма зависит от потребительских свойств товара, от финансового состояния покупателей и от других факторов. При этом
 (14)
(14)
– суммарный доход от продаж. А
 (15)
(15)
– так называемый предельный доход. Он определяет доход, полученный от единицы проданной продукции, если эта единица продана дополнительно к объему продаж q.
Эти и другие предельные величины широко используются в так называемом предельном экономическом анализе. В экономической литературе предельные величины называют также маржинальными. При их записи к обычному обозначению величин добавляется буква М. Например, MR – предельный доход R. И так как 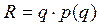 , то
, то
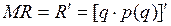 (16)
(16)
Производная функции, согласно ее математического определения (5) и (6) – это некий предел. Но, как и всякий предел, он может оказаться:
а) конечным; б) бесконечным; в) вообще не существовать.
Если для данного x имеет место вариант (а), то есть если при заданном x производная 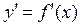 функции
функции  существует и конечна, то эта функция называется дифференцируемой в точке x.
существует и конечна, то эта функция называется дифференцируемой в точке x.
Функция, дифференцируемая в каждой точке x некоторого промежутка оси ох (например, интервала (a; b) или отрезка [ a; b ]) называется дифференцируемой на этом промежутке. Кстати, сама процедура вычисления производной функции называется ее дифференцированием (продифференцировать функцию – это значит найти ее производную).
 Из геометрического смысла производной функции, определяемого равенством (11) и рис.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции
Из геометрического смысла производной функции, определяемого равенством (11) и рис.5, вытекают следующие два наглядные необходимые и достаточные условия дифференцируемости заданной функции  в заданной точке x:
в заданной точке x:
1) Существование касательной к графику функции в его точке с абсциссой x.
2) Не вертикальность этой касательной (ибо 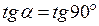 не существует).
не существует).
Например, функция  , график которой изображен на рис.7, не дифференцируема в точках x 1, x 2 и x 3.
, график которой изображен на рис.7, не дифференцируема в точках x 1, x 2 и x 3.
Действительно, точке x 1 соответствует на графике функции точка M 1 с вертикальной касательной. Точке x 2 (точке максимума функции) соответствует остроконечная вершина M 2, касательная в которой не существует. Точке x 3 соответствует точка M 3 – точка излома графика функции, в которой тоже касательная не существует.
Во всех же остальных точках M графика функции касательную к графику провести можно, и она не вертикальна. Значит, для всех остальных x, отличных от (x 1; x 2; x 3), существует производная функции. То есть во всех остальных точках x функция  дифференцируема.
дифференцируема.
Непрерывность функций.
Определение. Функция у=f(x) называется непрерывной при значении х=х0 (или в точке х0), если она определена в некоторой окрестности точки х0 (очевидно, и в самой точке х0) и если  или, что то же самое,
или, что то же самое, 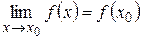 .
.
Геометрически непрерывность функции в данной точке означает, что разность ординат графика функции у=f(x) в точках  и х0 будет по абсолютной величине произвольно малой, если только
и х0 будет по абсолютной величине произвольно малой, если только  будет достаточно мало.
будет достаточно мало.
Для непрерывных функций справедливы следующие теоремы, регламентирующие операции с этими функциями:
Теорема 1: Если функции  и
и  непрерывны в точке х0, то сумма
непрерывны в точке х0, то сумма  также есть непрерывная функция в точке х0.
также есть непрерывная функция в точке х0.
Теорема 2: Произведение двух непрерывных функций есть функция непрерывная.
Теорема 3: Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.
Теорема 4: Если  непрерывна при
непрерывна при  и f(u) непрерывна в точке
и f(u) непрерывна в точке 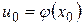 , то сложная функция
, то сложная функция  непрерывна в точке х0.
непрерывна в точке х0.
Еще три теоремы описывают свойства непрерывных функций:
Теорема 5: Если функция y=f(x) непрерывна на некотором отрезке  , то на отрезке
, то на отрезке  найдется по крайней мере одна точка
найдется по крайней мере одна точка 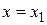 такая, что значение функции в этой точке будет удовлетворять соотношению
такая, что значение функции в этой точке будет удовлетворять соотношению , где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению
, где х – любая другая точка отрезка, и найдется по крайней мере одна точка х2 такая, что значение функции в этой точке будет удовлетворять соотношению  . Значение функции
. Значение функции 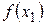 будем называть наибольшим значением функции y=f(x) на отрезке
будем называть наибольшим значением функции y=f(x) на отрезке  , значение функции
, значение функции  будем называть наименьшим значением функции на отрезке
будем называть наименьшим значением функции на отрезке  . (см. рис. 8)
. (см. рис. 8)

Рис. 8.
Теорема 6: Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и на концах этого отрезка принимает значения разных знаков, тогда между точками а и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль:
и на концах этого отрезка принимает значения разных знаков, тогда между точками а и b найдется по крайней мере одна точка х=с, в которой функция обращается в нуль: 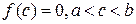 .
.
Геометрический смысл этой теоремы в том, что график непрерывной функции  , соединяющий точки
, соединяющий точки  и
и  , где
, где  и
и  (или
(или  и
и 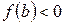 ) пересекает ось ох по крайней мере в одной точке.
) пересекает ось ох по крайней мере в одной точке.

Рис.9.
Теорема 7: Пусть функция  определена и непрерывна на отрезке
определена и непрерывна на отрезке . Если на концах этого отрезка функция принимает неравные значения
. Если на концах этого отрезка функция принимает неравные значения  , то каково бы ни было число
, то каково бы ни было число  , заключенное между числами А и В, найдется такая точка х=с, заключенная между а и b, что
, заключенное между числами А и В, найдется такая точка х=с, заключенная между а и b, что 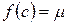 .
.
Геометрический смысл этой теоремы родственен теореме 6. В данном случае всякая прямая  пересекает график функции
пересекает график функции  .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 469; Нарушение авторских прав?; Мы поможем в написании вашей работы!