
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 24. Производная сложной функции и функции, заданной неявно. Производная обратной функции. Производная функции, заданной параметрически. Логарифмическое дифференцирование
|
|
|
|
Производная сложной функции.
Пусть 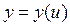 , а
, а  – любые две дифференцируемые функции своих аргументов. Тогда функция
– любые две дифференцируемые функции своих аргументов. Тогда функция  – так называемая сложная функция от x (она представляет собой функцию от функции). Найдем ее производную
– так называемая сложная функция от x (она представляет собой функцию от функции). Найдем ее производную 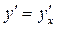 (производную от y по x). Для этого дадим аргументу x некоторое приращение
(производную от y по x). Для этого дадим аргументу x некоторое приращение  , то есть перейдем от x к
, то есть перейдем от x к  . Приращение
. Приращение  величины x вызовет некоторое приращение
величины x вызовет некоторое приращение  величины u, а то, в свою очередь, вызовет некоторое приращение
величины u, а то, в свою очередь, вызовет некоторое приращение 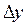 величины y. Так как функции
величины y. Так как функции 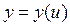 и
и  являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов. То есть при
являются, по условию, дифференцируемыми функциями своих аргументов, то они являются и непрерывными функциями своих аргументов. То есть при 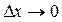 и
и 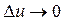 , и
, и  . А тогда, согласно определению производной, получаем:
. А тогда, согласно определению производной, получаем:
 .
.
Итак, если  – сложная функция от x, то
– сложная функция от x, то 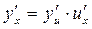 . Или, опуская значок x (но подразумевая его) запишем короче:
. Или, опуская значок x (но подразумевая его) запишем короче:
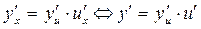 (1)
(1)
Формула (1) представляет собой правило вычисления производной (правило дифференцирования) сложной функции.
Собственно говоря, суть правила (1) проста. А именно, если функция 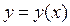 – простая функция от x (из числа основных элементарных функций, чьи производные содержатся в таблице производных), то ее производная и выглядит, и находится просто:
– простая функция от x (из числа основных элементарных функций, чьи производные содержатся в таблице производных), то ее производная и выглядит, и находится просто:  . А если
. А если 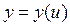 , где
, где  – две простых функции, то
– две простых функции, то  – уже сложная функция от x. Ее производная
– уже сложная функция от x. Ее производная  по x находится уже по формуле (1): сначала находим производную от функции
по x находится уже по формуле (1): сначала находим производную от функции 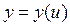 по переменной u (точно так же, как находим производную от функции
по переменной u (точно так же, как находим производную от функции 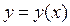 по переменной x), а затем умножаем ее на производную функции
по переменной x), а затем умножаем ее на производную функции  по переменной x.
по переменной x.
Чтобы сделать наглядным применение этого правила, приведем таблицу сравнения, содержащую производные некоторых простых и аналогичных им сложных функций от x:
Таблица 1.
| Производные простых функций (x – независимая переменная) | Производные сложных функций
( – любая
дифференцируемая функция) – любая
дифференцируемая функция)
| |
1. 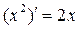
| 1. 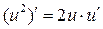
| |
2. 
| 2.
| |
3. 
| 3. 
| |
4. 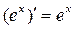
| 4. 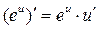
| |
5. 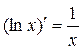
| 5. 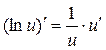
| |
6. 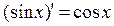
| 6. 
| |
| (……) | (……) |
Таблица (1) наглядно иллюстрирует разницу между производными простых и сложных функций.
Пример 1. 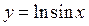 ;
; 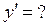
Решение.
Пример 2. 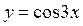 ;
; 
Решение.
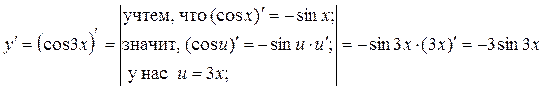
Пример 3.  ;
; 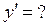
Решение.

Пример 4. 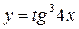 ;
; 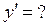
Решение.

 .
.
Пусть теперь 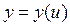 и
и  – любые две дифференцируемые функции. Тогда
– любые две дифференцируемые функции. Тогда  – сложная функция от x. И ее дифференциал dy, как оказывается, можно найти по любой из двух следующих формул:
– сложная функция от x. И ее дифференциал dy, как оказывается, можно найти по любой из двух следующих формул:
1) 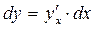 ; 2)
; 2) 
Данные формулы выражают так называемое свойство инвариантности формы дифференциала функции. Согласно этого свойства, дифференциал функции имеет форму произведения производной этой функции на дифференциал ее аргумента независимо от того, является ли ее аргумент независимой переменной (x) или функцией (u) от другого аргумента.
Действительно, если x – независимая переменная, то дифференциал dy функции y, зависящей от x, находится, по первой из этих формул. Но так как  – сложная функция от x, то используя формулу (1) для производной сложной функции, получим:
– сложная функция от x, то используя формулу (1) для производной сложной функции, получим:
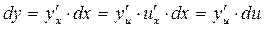
То есть приходим ко второй формуле.
Производная функции, заданной неявно.
Если функция  задана в неявном виде, то есть задана уравнением
задана в неявном виде, то есть задана уравнением 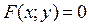 (в этом уравнении y не выражен через x, и выразить его не удается), то при нахождении производной
(в этом уравнении y не выражен через x, и выразить его не удается), то при нахождении производной  такой функции поступают следующим образом:
такой функции поступают следующим образом:
1) Дифференцируют обе части уравнения 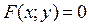 по x, помня при этом, что y – это функция от x. В результате появляется некоторое равенство
по x, помня при этом, что y – это функция от x. В результате появляется некоторое равенство 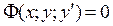 , содержащее искомую производную
, содержащее искомую производную  .
.
2) Выражают из полученного равенства эту производную.
Таким образом, производную  функции y, заданной неявно уравнением
функции y, заданной неявно уравнением 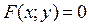 , находят по схеме:
, находят по схеме:
 (2)
(2)
Пример 5. Найти производную  функции y, заданной неявно уравнением
функции y, заданной неявно уравнением  .
.
Решение.



Производная функции, заданной параметрически.
Если функция задана в параметрической форме
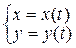 , (3)
, (3)
то ее производную  находят по формуле:
находят по формуле:
 . (4)
. (4)
Подтвердим эту формулу. Пусть 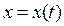 и
и  – дифференцируемые функции параметра t. Зафиксируем некоторое t, а затем придадим ему приращение
– дифференцируемые функции параметра t. Зафиксируем некоторое t, а затем придадим ему приращение 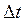 . При этом x и y получат некоторые приращения
. При этом x и y получат некоторые приращения 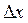 и
и 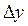 , причем при
, причем при  и
и 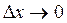 , и
, и 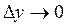 (функции
(функции 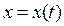 и
и  – дифференцируемые, а значит, и непрерывные). А тогда
– дифференцируемые, а значит, и непрерывные). А тогда
 .
.
Пример 6. Функция 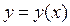 , заданная параметрически уравнениями
, заданная параметрически уравнениями
 ,
,
представляет собой параметрическое уравнение окружности с центром в начале координат и радиусом R (рис. 1).
Найдем производную  этой функции:
этой функции:

|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1443; Нарушение авторских прав?; Мы поможем в написании вашей работы!