
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Упражнения
|
|
|
|
Физический смысл производной второго порядка.
Если 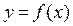 – уравнение движения точки по ее траектории, то, как мы знаем, ее производная
– уравнение движения точки по ее траектории, то, как мы знаем, ее производная  (производная первого порядка) представляет собой скорость v (x) движения точки (мгновенную скорость движения). Но тогда производная второго порядка
(производная первого порядка) представляет собой скорость v (x) движения точки (мгновенную скорость движения). Но тогда производная второго порядка  будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому
будет иметь смысл «скорость изменения скорости» движения точки. В физике такая величина называется ускорением. Поэтому
 (3)
(3)
– ускорение движения точки в момент x. В этом и состоит физический смысл производной второго порядка.
Пример 4. Как известно, уравнение движения свободно падающего в безвоздушном пространстве тела, начавшего свое падение в момент 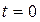 , имеет вид:
, имеет вид: 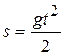 (s – путь, пройденный падающим телом за время t). Найдем скорость
(s – путь, пройденный падающим телом за время t). Найдем скорость 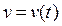 и ускорение
и ускорение 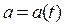 падающего тела:
падающего тела:
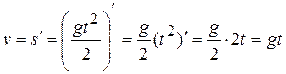 ;
;
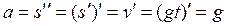 .
.
То есть ускорение a падающего тела неизменно и равно g – ускорению свободного падения ( м/сек2). А скорость v падающего тела возрастает пропорционально времени по формуле
м/сек2). А скорость v падающего тела возрастает пропорционально времени по формуле  .
.
1. Найти угол наклона к оси ох касательной, проведенной к параболе  в точке
в точке  .
.
Ответ: 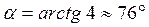 .
.
2. Найти на параболе  такую точку
такую точку  , чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол
, чтобы касательная к параболе, проведенная в этой точке, составила с осью ох угол  .
.
Ответ: 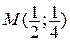 .
.
3. В момент времени 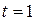 найти скорость v и ускорение a точки, движущейся по оси ох по закону
найти скорость v и ускорение a точки, движущейся по оси ох по закону 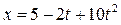 .
.
Ответ: 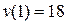 ;
;  .
.
4. Найти производную  функций:
функций:
а)  ; б)
; б) 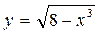 ; в)
; в) 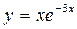 ; г)
; г) 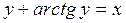 ; д)
; д) 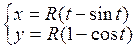
Ответ: а)  ; б)
; б) 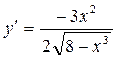 ; в)
; в) 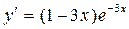 ;
;
г) 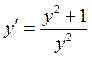 ; д)
; д)  .
.
5. Найти производную  функций:
функций:
а) 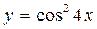 ; б)
; б)  ; в)
; в) 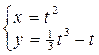 .
.
Ответ: а)  ; б)
; б)  ; в)
; в)  .
.
Правило Лопиталя вычисления пределов.
Это правило состоит в следующем. Если требуется найти предел вида
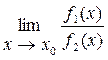 , (4)
, (4)
где x0 – число или символ 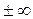 , и этот предел приводит к неопределенности вида
, и этот предел приводит к неопределенности вида  или
или 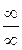 , то
, то
 , (5)
, (5)
Словесная формулировка правила Лопиталя (5) такова: предел отношения бесконечно малых или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует.
Доказательство. Исчерпывающее доказательство правила Лопиталя довольно громоздко. В связи с этим ограничимся рассмотрением случая, когда предел (4) приводит к неопределенности вида  :
:
 ;
; 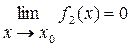 ;
;  . (6)
. (6)
При этом будем считать, что x 0 – некоторое конечное число.
Если функции  и
и  непрерывны в точке x 0, то в силу определения непрерывности функций верны следующие равенства
непрерывны в точке x 0, то в силу определения непрерывности функций верны следующие равенства 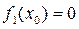 и
и  . Если же эти функции в точке x 0 разрывны, то их значения при x 0 не равны нулю (у них другие значения или они там вообще не определены). Тогда переопределим (или доопределим) их в точке x 0 так, чтобы стало
. Если же эти функции в точке x 0 разрывны, то их значения при x 0 не равны нулю (у них другие значения или они там вообще не определены). Тогда переопределим (или доопределим) их в точке x 0 так, чтобы стало 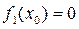 и
и  . После этого, в силу того же определения непрерывности функций, функции
. После этого, в силу того же определения непрерывности функций, функции  и
и  станут непрерывными в точке x 0. Далее, будем считать, что обе эти функции будут непрерывно дифференцируемыми в окрестности точки х0, включая саму точку х0, причем
станут непрерывными в точке x 0. Далее, будем считать, что обе эти функции будут непрерывно дифференцируемыми в окрестности точки х0, включая саму точку х0, причем  . Тогда получим:
. Тогда получим:
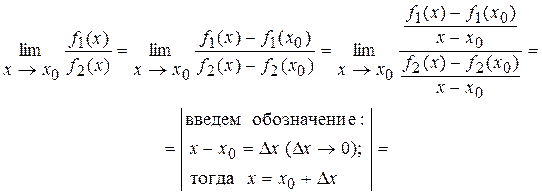


Примечание. Предел отношения производных, стоящий в правой части равенства (5), тоже может приводить к неопределенности вида  или
или 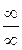 . Тогда правило Лопиталя можно применить и к нему. То есть применить это правило повторно.
. Тогда правило Лопиталя можно применить и к нему. То есть применить это правило повторно.
Пример 5.
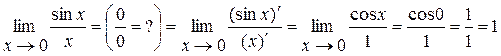 .
.
Пример 6.
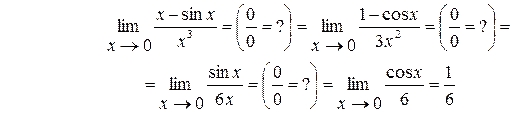
Пример 7.
 .
.
Пример 8.

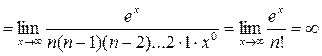 .
.
Последние два примера показывают, что при 
 растет несравненно медленнее, чем x, а
растет несравненно медленнее, чем x, а 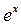 – несравненно быстрее, чем
– несравненно быстрее, чем 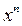 при любом значении n.
при любом значении n.
Пример 9.
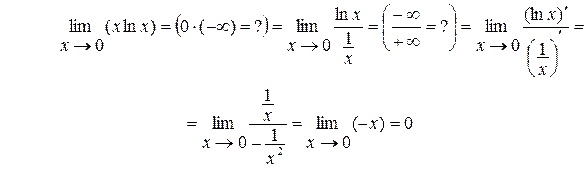
Пример 10.  .
.
Для вычисления этого предела введем обозначение:  . Тогда
. Тогда 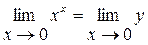 . Учитывая, что
. Учитывая, что 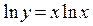 , находим:
, находим:
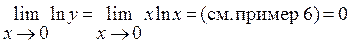
Итак,  . То есть при
. То есть при 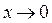 и
и  , а значит,
, а значит,  , ибо
, ибо 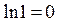 . Таким образом,
. Таким образом,  , а значит,
, а значит, 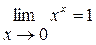 .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 334; Нарушение авторских прав?; Мы поможем в написании вашей работы!