
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формулы Маклорена и Тейлора
|
|
|
|
Упражнения
1. Найти дифференциалы первого и второго порядков следующих функций:
а) 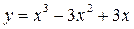 ; б)
; б) 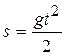 ; в)
; в)  , где u – дифференцируемая функция некоторой независимой переменной.
, где u – дифференцируемая функция некоторой независимой переменной.
Ответ:
а) 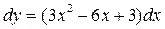 ;
; 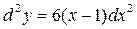 .
.
б) 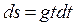 ;
; 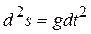 .
.
в) 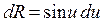 ;
; 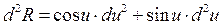 .
.
2. С помощью приближенной формулы 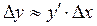 найти абсолютную и относительную погрешности вычисления объема куба со стороной x, если при измерении x допущена ошибка
найти абсолютную и относительную погрешности вычисления объема куба со стороной x, если при измерении x допущена ошибка 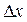 .
.
Ответ: 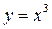 ;
;
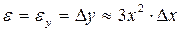 – абсолютная погрешность;
– абсолютная погрешность;
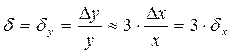 – относительная погрешность.
– относительная погрешность.
В предыдущем параграфе был получен простейший вариант формулы Тейлора: 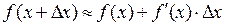 . Эта формула приближенная, и она тем точнее, чем меньше
. Эта формула приближенная, и она тем точнее, чем меньше  . Но хотелось бы знать больше. Хотелось бы иметь оценку погрешности этой формулы. А еще лучше – иметь возможность заменить эту формулу на более точную, такую, чтобы ее погрешностью заведомо можно было бы пренебречь. С этой целью проведем в формуле
. Но хотелось бы знать больше. Хотелось бы иметь оценку погрешности этой формулы. А еще лучше – иметь возможность заменить эту формулу на более точную, такую, чтобы ее погрешностью заведомо можно было бы пренебречь. С этой целью проведем в формуле 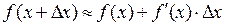 переобозначения:
переобозначения:
· старое обозначение x – новое обозначение x 0;
· старое обозначение  – новое обозначение x;
– новое обозначение x;
· старое обозначение 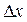 – новое обозначение
– новое обозначение 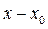 .
.
Тогда эта формула примет вид:
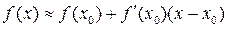 (11)
(11)
То есть получаем приближенную формулу вида
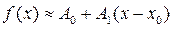 , (12)
, (12)
где 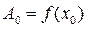 ;
; 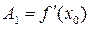 . Использование этой приближенной формулы равносильно замене кривой
. Использование этой приближенной формулы равносильно замене кривой 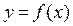 на прямую с уравнением
на прямую с уравнением 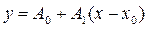 , которая является касательной, проведенной к графику функции
, которая является касательной, проведенной к графику функции 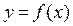 в точке M 0 с абсциссой x 0 (рис. 1).
в точке M 0 с абсциссой x 0 (рис. 1).
Действительно, прямая 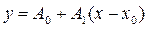 проходит через точку
проходит через точку 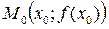 . Кроме того, она имеет угловой коэффициент
. Кроме того, она имеет угловой коэффициент 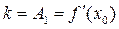 . А это и есть, согласно геометрического смысла производной (см. 1.11), угловой коэффициент касательной, проведенной к графику функции
. А это и есть, согласно геометрического смысла производной (см. 1.11), угловой коэффициент касательной, проведенной к графику функции 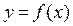 в точке M 0. Для
в точке M 0. Для 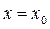 приближенная формула (12) становится точной. А для
приближенная формула (12) становится точной. А для 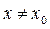 она, очевидно, тем точнее, чем ближе x к x 0.
она, очевидно, тем точнее, чем ближе x к x 0.
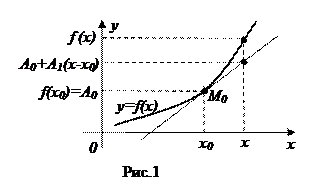 Для x, очень близких к x 0, замена кривой
Для x, очень близких к x 0, замена кривой 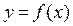 на касательную к ней, или как еще говорят, аппроксимация кривой её касательной, очевидно, вполне оправдана. Но с удалением x от x 0 расхождение между кривой и касательной к ней может стать существенным, а формула (12) может стать слишком грубой.
на касательную к ней, или как еще говорят, аппроксимация кривой её касательной, очевидно, вполне оправдана. Но с удалением x от x 0 расхождение между кривой и касательной к ней может стать существенным, а формула (12) может стать слишком грубой.
Возникает естественная мысль: поискать замену кривой не на прямую, а на другую кривую, только более простую (на параболу, гиперболу, и т.д.). В соответствии с этой мыслью приближенные значения функции 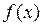 для x, близких к x 0, будем искать по обобщению формулы (12):
для x, близких к x 0, будем искать по обобщению формулы (12):
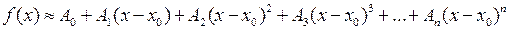 (13)
(13)
В простейшем случае 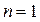 формула (13) совпадает формулой (12). А при
формула (13) совпадает формулой (12). А при 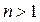 мы вправе ожидать, что формула (13) окажется более точной, чем формула (12), и что ее точность будет возрастать с увеличением числа n. Действительно, аппроксимация кривой
мы вправе ожидать, что формула (13) окажется более точной, чем формула (12), и что ее точность будет возрастать с увеличением числа n. Действительно, аппроксимация кривой 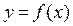 параболой (при
параболой (при 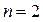 ), кубической параболой (при
), кубической параболой (при 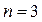 ) и т.д. более естественна, чем аппроксимация кривой какой угодной прямой. И чем сложнее аппроксимирующая кривая, тем качественнее может быть осуществлена эта аппроксимация. В том числе и для x, достаточно удаленных от x 0.
) и т.д. более естественна, чем аппроксимация кривой какой угодной прямой. И чем сложнее аппроксимирующая кривая, тем качественнее может быть осуществлена эта аппроксимация. В том числе и для x, достаточно удаленных от x 0.
Потребуем, чтобы формула (13), как и ее частный случай (12), была точной при 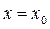 . Тогда получим:
. Тогда получим:
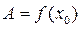 (14)
(14)
Найдем остальные коэффициенты 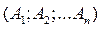 формулы (13). Предположим, что функцию
формулы (13). Предположим, что функцию 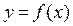 можно сколько угодно раз дифференцировать в некоторой окрестности точки
можно сколько угодно раз дифференцировать в некоторой окрестности точки 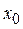 , и продифференцируем обе части приближенного равенства (13) до n -го порядка включительно:
, и продифференцируем обе части приближенного равенства (13) до n -го порядка включительно:
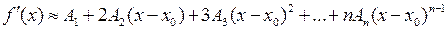 ;
;
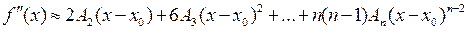 ; (15)
; (15)
-------------------------------------------------------------------------
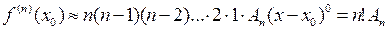
Здесь использовано обозначение:
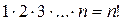 (эн – факториал) (16)
(эн – факториал) (16)
В частности,
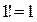 ;
; 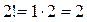 ;
; 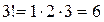 ; …
; … 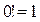 (по определению) (17)
(по определению) (17)
Приближенные равенства (15), как и исходное равенство (13), должны быть тем точнее, чем ближе x к x 0. Потребовав, чтобы при 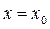 все они стали точными, получим:
все они стали точными, получим:
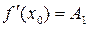 ;
; 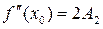 ;
; 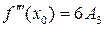 ; …
; … 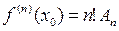
Отсюда
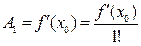 ;
; 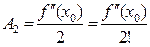 ;
; 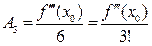 ; …
; … 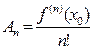 (18)
(18)
Подставляя выражения (18) в (13), получим для x, близких к x 0:
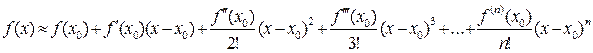 (19)
(19)
Полученная ранее формула (11) является простейшим частным случаем этой формулы при 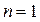 .
.
Формула (19) – приближенная. Следует ожидать, что ее точность должна повышаться как при приближении x к x 0, так и при увеличении числа ее слагаемых n. Но чтобы убедиться в этом окончательно, следует получить оценку погрешности этой формулы для всех n, начиная с 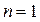 .
.
Обозначим символом 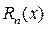 эту погрешность (
эту погрешность (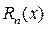 – разность между левой и правой частями формулы (19)). Тогда получим точно для любых х и n:
– разность между левой и правой частями формулы (19)). Тогда получим точно для любых х и n:
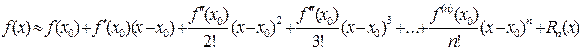 (20)
(20)
Формула (20) называется формулой Тейлора. Последнее слагаемое 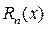 называется остаточным членом формулы Тейлора. Поэтому еще говорят, что (20) – это формула Тейлора с остаточным членом.
называется остаточным членом формулы Тейлора. Поэтому еще говорят, что (20) – это формула Тейлора с остаточным членом.
При практическом использовании формулы Тейлора ее остаточный член отбрасывают, переходя тем самым к приближенной формуле (19), которую называют формулой Тейлора без остаточного члена. А для правомерности отбрасывания (игнорирования) остаточного члена 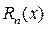 используют его оценку, полученную французским математиком 19-го века Лагранжем:
используют его оценку, полученную французским математиком 19-го века Лагранжем:
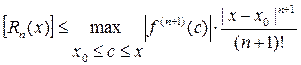 (21)
(21)
Если 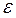 – допустимая погрешность вычисления функции
– допустимая погрешность вычисления функции 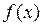 , то для данных x и x 0 подбирают такое значение n, чтобы
, то для данных x и x 0 подбирают такое значение n, чтобы 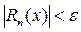 .
.
При 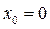 формула Тейлора (20) принимает вид
формула Тейлора (20) принимает вид
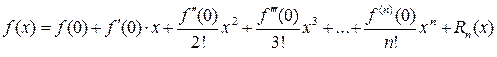 (22)
(22)
и называется формулой Маклорена. Ее остаточный член 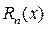 оценивается по формуле (23), вытекающей из (21) при
оценивается по формуле (23), вытекающей из (21) при 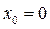 :
:
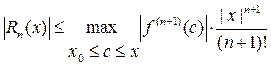 (23)
(23)
Формулой Маклорена, после оценки и отбрасывания ее остаточного члена, пользуются для приближенного вычисления значений 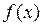 при x, близких к нулю.
при x, близких к нулю.
Пример 11. Вычислить  с точностью до 0,001.
с точностью до 0,001.
Решение. Рассмотрим функцию 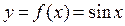 (x – в радианах). Тогда
(x – в радианах). Тогда 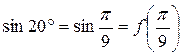 . То есть
. То есть 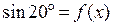 при
при 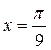 . Так как
. Так как 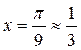 и близок к нулю, то для приближенного вычисления
и близок к нулю, то для приближенного вычисления  воспользуется формулой Маклорена (22). Но для этого сначала нужно найти такое значение n, чтобы остаточный член
воспользуется формулой Маклорена (22). Но для этого сначала нужно найти такое значение n, чтобы остаточный член  этой формулы по абсолютной величине был заведомо меньше 0,001. Тогда, отбросив его в формуле Маклорена (22) и подсчитав сумму оставшихся слагаемых, получим нужное значение
этой формулы по абсолютной величине был заведомо меньше 0,001. Тогда, отбросив его в формуле Маклорена (22) и подсчитав сумму оставшихся слагаемых, получим нужное значение 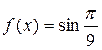 с точностью до 0,001.
с точностью до 0,001.
Сначала оценим первый множитель в формуле (23):
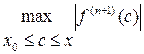 . (24)
. (24)
Имеем:
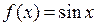 ;
;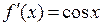
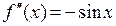 ;
; 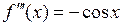 ;
; 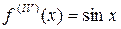 …
…
Таким образом, производные функции 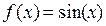 любого порядка равны либо
любого порядка равны либо 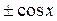 , либо
, либо 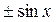 . А значит, при любых x они по абсолютной величине не превосходят единицы. Следовательно, при любых
. А значит, при любых x они по абсолютной величине не превосходят единицы. Следовательно, при любых 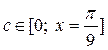 и любых n имеем:
и любых n имеем:
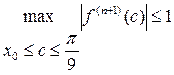 (25)
(25)
С учетом (25) оценка (23) остаточного члена формулы Маклорена при 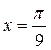 принимает вид:
принимает вид:
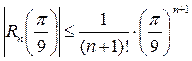 (n = 1, 2,…) (26)
(n = 1, 2,…) (26)
Оценим значение правой части этого неравенства при различных n:
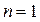 ;
; 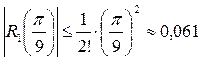 ;
;
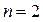 ;
; 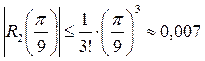 ;
;
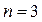 ;
; 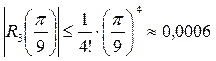 .
.
Для 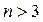 правая часть неравенства (26), а следовательно, и его левая часть, т еще меньше, чем при
правая часть неравенства (26), а следовательно, и его левая часть, т еще меньше, чем при 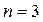 . Таким образом, если мы возьмем
. Таким образом, если мы возьмем 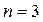 , то
, то 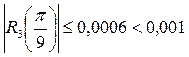 – это нас устроит. Тогда записывая формулу Маклорена (22) для
– это нас устроит. Тогда записывая формулу Маклорена (22) для 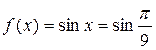 при
при 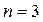 и отбрасывая в ней остаточный член, получим:
и отбрасывая в ней остаточный член, получим:
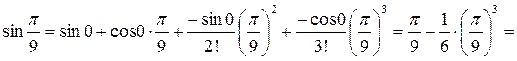
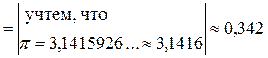
Итак, 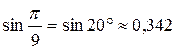 – с точностью до 0,001. Сверяя это значение с табличным (по таблице Брадиса
– с точностью до 0,001. Сверяя это значение с табличным (по таблице Брадиса 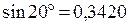 ), видим, что у нас нет расхождения даже в десятитысячных.
), видим, что у нас нет расхождения даже в десятитысячных.
Кстати, если бы в формуле Маклорена (22) мы взяли 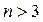 (
(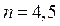 , и т.д.), то получили бы значение
, и т.д.), то получили бы значение  еще точнее. В принципе – как угодно точно.
еще точнее. В принципе – как угодно точно.
Совершенно аналогично с помощью формулы Маклорена (если x близок к 0), или с помощью формулы Тейлора (если x далек от 0, но близок к некоторому удобному для расчетов значению x 0), можно вычислять приближенные значения 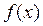 и других многократно дифференцируемых функций. Именно на использовании этих формул и основано составление таблиц значений различных функций.
и других многократно дифференцируемых функций. Именно на использовании этих формул и основано составление таблиц значений различных функций.
Для различных расчетов удобно пользоваться разложениями элементарных функций в ряд Маклорена. Приведем некоторые, наиболее широко используемые разложения:
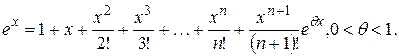
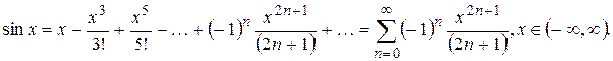
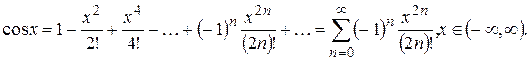
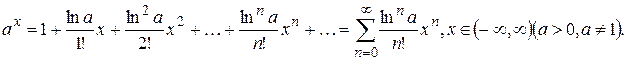
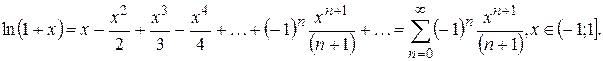
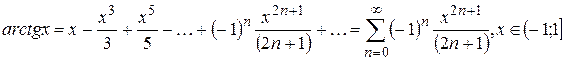
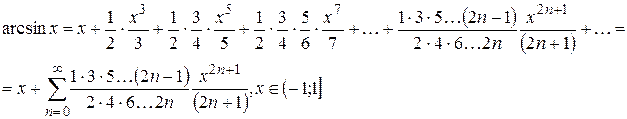
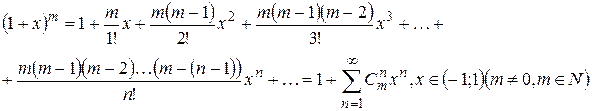
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 720; Нарушение авторских прав?; Мы поможем в написании вашей работы!