Предел и непрерывность функции

Основные понятия

Дифференциальное исчисление функции одной переменной.

Пусть D — некоторое множество чисел. Если задан закон, по которому каждому числу x из множества D ставится в соответствие единственное определенное число y, то будем говорить, что на множестве D задана функция, которую назовём f. Число y — это значение функции f в точке x, что обозначается формулой y = f(x).

Число x называется аргументом функции, множество D — областью определения функции, а все значения y образуют множество E, которое называется множеством значений или областью изменения функции.

В окружающем нас мире очень много таких зависимостей. У них есть общее свойство — при некоторых небольших частных изменениях меняется и общая ситуация. В математике подобное свойство называют непрерывностью. Если же ситуация такова, что небольшое изменение параметров кардинально меняет всю ситуацию, то ситуацию можно назвать кризисной.

Поэтому важно научиться изучать функции.

Перечислим свойства функций, известные из школы — область определения; область изменения; чётность, нечётность или общего вида; периодичность; характерные точки; экстремальные точки; участки монотонности; асимптоты.

Удобен графический способ представления функций. Графиком функции f(x) называется множество точек координатной плоскости с координатами (x, f(x)). Приведём некоторые из них — известные вам и совсем не известные:

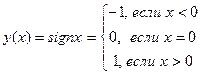
Чтобы изучать поведение функций введём понятие e – окрестности точки x₀.

Так как между множеством действительных чисел и множеством точек числовой оси можно установить взаимно-однозначное соответствие, в дальнейшем изложении понятиям “число х ”и “точка х числовой оси” в некоторых случаях будет придаваться один и тот же смысл. Например, вместо “значение функции при значении аргумента, равном х ₁” будет говориться “значение функции в точке х ₁”. В нижеследующем определении можно везде заменить выражение “точка х ” на выражение “число х ”.

Пусть e — некоторое положительное число. e – окрестностью точки x₀ называется множество всех точек x, принадлежащих промежутку (x₀ ‑ e, x₀ + e), кроме самой точки x₀.

Принадлежность точки x e ‑ окрестности точки можно выразить с помощью двойного неравенства 0 < êx – x₀ç < e. Число e называется радиусом окрестности.

Рассмотрим функцию y = x ² в точке x ₀ = 2. Значение функции в этой точке равно 4.

Отметим одну особенность поведения функции в этой точке. Можно

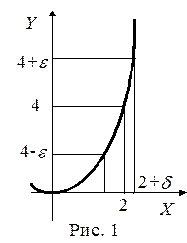
выбрать какое-либо положительное число eи построить e - окрестность точки y ₀ = 4. Очевидно, что найдется такая окрестность точки x ₀ = 2 (на Рис. 1 эта окрестность имеет радиус d), что если x будет лежать в этой окрестности, то соответствующее значение y, равное x ², попадет в e – окрестность точки y ₀ = 4. Это заключение справедливо для любого, сколь угодно малого числа e. Здесь точка x ₀ = 2 выбрана произвольно. Можно было бы для данной функции выбрать любую другую точку и сделать подобное заключение.

Рассмотрим функцию 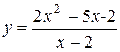. Эта функция не определена в точке x ₀ = 2. При x ₀ ¹ 2 её можно преобразовать:

.

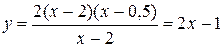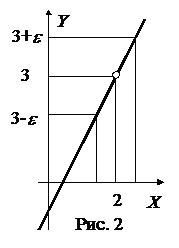График функции представлен на Рис. 2. Хотя исходная функция не определена в точке x ₀ = 2 и естественно не равна 3 в этой точке, точка y ₀ = 3 имеет характерную особенность. Выбрав положительное число e, можно утверждать, что если рассматривать значения x, расположенные достаточно близко к точке x ₀ = 2 (или лежащие в некоторой окрестности точки x ₀ = 2, причем радиус этой окрестности зависит от e), то соответствующие значения y попадут в e-окрестность точки y ₀ = 3. Всё сказанное остаётся справедливым независимо от того, насколько малым выбрано положительное число e.

Введем понятие предела функции. Число A называется пределом функции y = f(x) в точке x₀ (иногда говорят, при x, стремящемся к x₀), если для любого положительного числа e можно найти такое положительное число d, что для всех x из d – окрестности точки x₀ соответствующие значения y попадают в e – окрестность точки y = A.

Можно сформулировать определение предела функции по-другому. Число A называется пределом функции y = f(x) в точке x₀, если для любого положительного числа e можно найти такое положительное число d, что для всех x, удовлетворяющих условию

0 < ê x – x ₀ê < d, выполняется условие ê y – A ê < e.

Тот факт, что A есть предел функции y = f (x) в точке x = x ₀, записывается формулой .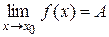

.

Как видно из второго из рассмотренных выше примеров, для того, чтобы функция имела предел в точке x = x ₀, не требуется, чтобы она была определена в этой точке.

Рассмотрим функцию 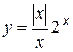. Очевидно, что если x > 0, то y = 2 ^x; если x < 0, то y = – 2 ^x; при x = 0 функция не определена.

График функции изображен на Рис. 3. Легко убедиться в том, что, согласно приведенному выше определению предела, эта функция в точке x = 0 предела не имеет.

Функция y = f(x) называется непрерывной в точке x = x₀, если она определена в этой точке и ее значение f(x₀) равно пределу функции в этой точке: .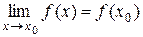

Функция y = x ² непрерывна в точке x = 2, как и во всех точках числовой оси. Функция 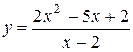не является непрерывной в точке x = 2. Функция 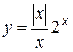не является непрерывной в точке x = 0.

Функция, непрерывная в каждой точке открытого промежутка, называется непрерывной на этом промежутке.

Приведем свойства предела функции.

1. Функция не может иметь в одной точке два разных предела.

2. 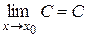, если C — постоянная функция.

3. Если существует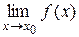и C — постоянная функция, то

.

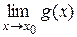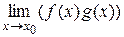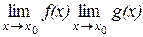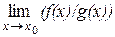4. Если существуюти , то существует , равный , а также существует , равный . Если при этом , то существует, равный .

Введем определения так называемых “односторонних пределов”.

Число B называется пределом функции f(x) в точке a справа (это записывается в виде формулы ), если для любого поло­жительного числа e найдется положительное число d, такое что из из условия 0 < x – a < d будет следовать ê B –f (x) ê < e.

Согласно приведенному определению . Отметим, что обыкновенного предела функция 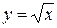в точке x = 0 не имеет.

Число С называется пределом функции f(x) в точке b слева (это записывается в виде формулы 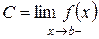), если для любого поло­жительного числа e найдется положительное число d такое, что из условия 0 < b – x < d будет следовать ê C – f (x)ê < e.

Очевидно, что функция 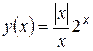(её график, изображен на Рис. 3) имеет два односторонних предела в точке x = 0:

; .

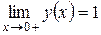Функция f(x) называется непрерывной в точке a справа (непрерывной в точке b слева), если

().

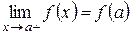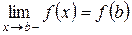Функция непрерывна справа в точке x =0.

Функция называется непрерывной на замкнутом промежутке [ a, b ], если она непрерывна на открытом промежутке (a, b), непрерывна справа в точке a и непрерывна слева в точке b.

Достаточно просто можно доказать теорему, связывающую понятия предела функции в точке и односторонних пределов. Мы ограничимся только формулировкой теоремы.

Для того, чтобы выполнялось равенство 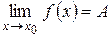, необходимо и достаточно, чтобы одновременно выполнялись два равенства:

; .

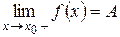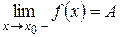В дальнейшем нам понадобятся понятия предела функции в бесконечно удалённых точках. Рассмотрим сначала функцию f (x), определенную на полубесконечном промежутке (х ₀; ¥). Число А называется пределом функции f(x) при х, стремящемся к бесконечности:

,

если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, превосходящих М, выполняется условие:

½ f (x) – A ½ < e.

Пусть теперь функция f (x) определена на полубесконечном промежутке
(–¥; х ₀ ). Число А называется пределом функции f(x) при х, стремящемся к минус бесконечности:

,

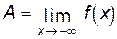если для любого положительного числа e можно найти такое положительное число M (зависящее от e), что для всех чисел х, меньших, чем – М, выполняется условие:

½ f (x) – A ½ < e.

Отметим два, так называемых, "замечательных предела".

1. . Геометрический смысл этой формулы заключается в том, что прямая 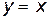является касательной к графику функции 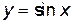в точке .

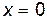2. 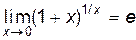. Здесь e — иррациональное число, приблизительно равное 2,72.

Приведем пример применения понятия предела функции в экономических расчетах. Рассмотрим обыкновенную финансовую сделку: предоставление в долг суммы S ₀ с условием, что через период времени T будет возвращена сумма S_T. Определим величину r относительного роста формулой

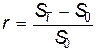. (1)

Относительный рост можно выразить в процентах, умножив полученное значение r на 100.

Из формулы (1) легко определить величину S_T: S_T = S ₀(1 + r)

При расчете по долгосрочным кредитам, охватывающим несколько полных лет, используют схему сложных процентов. Она состоит в том, что если за 1-й год сумма S ₀ возрастает в (1 + r) раз, то за второй год в (1 + r) раз возрастает сумма S ₁ = S ₀(1 + r), то есть S ₂ = S ₀(1 + r)². Аналогично получается S ₃ = S ₀(1 + r)³. Из приведенных примеров можно вывести общую формулу для вычисления роста суммы за n лет при расчете по схеме сложных процентов: S_n = S ₀(1 + r) ⁿ.

В финансовых расчетах применяются схемы, где начисление сложных процентов производится несколько раз в году. При этом оговариваются годовая ставка r и количество начислений за год k. Как правило, начисления производятся через равные промежутки времени, то есть длина каждого промежутка T_k составляет 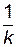часть года. Тогда для срока в T лет (здесь T не обязательно является целым числом) сумма S_T рассчитывается по формуле

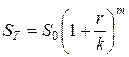(2)

Здесь 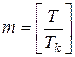— целая часть числа 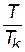, которая совпадает с самим числом, если, например, T ‑ целое число.

Пусть годовая ставка равна r и производится n начислений в год через равные промежутки времени. Тогда за год сумма S ₀ наращивается до величины, определяемой формулой

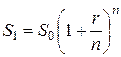(3)

В теоретическом анализе и в практике финансовой деятельности часто встречается понятие “непрерывно начисляемый процент”. Чтобы перейти к непрерывно начисляемому проценту, нужно в формулах (2) и (3) неограниченно увеличивать соответственно, числа k и n (то есть устремить k и n к бесконечности) и вычислить, к какому пределу будут стремиться функции S_T и S ₁. Применим эту процедуру к формуле (3):

.

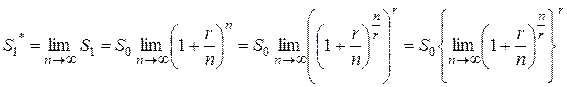Заметим, что предел в фигурных скобках совпадает со вторым замечательным пределом. Отсюда следует, что при годовой ставке r при непрерывно начисляемом проценте сумма S ₀ за 1 год наращивается до величины S ₁^*, которая определяется из формулы

S ₁^* = S ₀ e^r. (4)

Пусть теперь сумма S ₀ предоставляется в долг с начислением процента n раз в год через равные промежутки времени. Обозначим r_e годовую ставку, при которой в конце года сумма S ₀ наращивается до величины S ₁^* из формулы (4). В этом случае будем говорить, что r_e — это годовая ставка при начислении процента n раз в год, эквивалентная годовому проценту r при непрерывном начислении. Из формулы (3) получаем

.

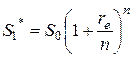Приравнивая правые части последней формулы и формулы (4), полагая в последней T = 1, можно вывести соотношения между величинами r и r_e:

, .

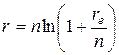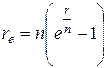Эти формулы широко используются в финансовых расчётах.

Дата добавления: 2013-12-13