Производная

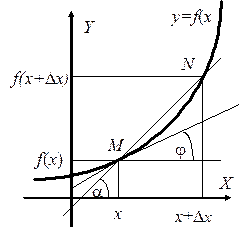
Рассмотрим функцию y=f (x), непрерывную в некоторой окрестности точки x. Пусть D x - приращение аргумента в точке x. Обозначим через Dy или D f приращение функции, равное f (x +D x) – f (x). Отметим здесь, что функция непрерывна в точке x, если в этой точке бесконечно малому приращению аргу­мента D x соответствует бесконечно малое приращение функции D f.

Отношение D f /D x, как видно из рисунка, равно тангенсу угла a, который составляет секущая MN кривой y = f (x) c положительным направлением горизонтальной оси координат.

Представим себе процесс, в котором величина D x, неограниченно уменьшаясь, стремится к нулю. При этом точка N будет двигаться вдоль кривой y = f (x), приближаясь к точке M, а секущая MN будет вращаться около точки M так, что при очень малых величинах D x её угол наклона a будет сколь угодно близок к углу j наклона касательной к кривой в точке x. Следует отметить, что все сказанное относится к случаю, когда график функции y = f (x) не имеет излома или разрыва в точке x, то есть в этой точке можно провести касательную к графику функции.

Отношение D y / D x или, что то же самое (f (x + D x) - f (x)) / D x, можно рассматривать при заданном x как функцию аргумента D x. Эта функция не определена в точке D x = 0. Однако её предел в этой точке может существовать.

Если существует предел отношения (f (x + D x) – f (x)) / D x в точке D x = 0, то он называется производной функции y = f (x) в точке x и обозначается y¢ или f¢ (x):

.

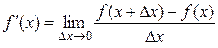Нахождение производной функции y = f(x) называется дифференцированием.

Если для любого числа x из открытого промежутка (a, b) можно вычислить f¢(x), то функция f(x) называется дифференцируемой на промежутке (a, b).

Геометрический смысл производной заключается в том, что произ­водная функции f(x) в точке x равна тангенсу угла наклона касательной к графику функции в этой точке.

Производная - это скорость изменения функции в точке x. Из определения производной следует, что f¢ (x)» D f / D x, причем точность этого приближенного равенства тем выше, чем меньше D x. Производная f¢ (x) является приближенным коэффициентом пропорциональности между D f и D x.

Производная функции f (x) не существует в тех точках, в которых функция не является непрерывной. В то же время функция может быть непрерывной в точке x ₀, но не иметь в этой точке производной. Такую точку назовём угловой точкой графика функции или точкой излома. Графические примеры приведены на рисунках:

Так функция y = ê x ê не имеет производной в точке x = 0, хотя является непрерывной в этой точке.

Ниже приводится таблица производных элементарных функций.

f (x)		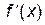f (x)		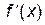f (x)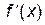
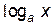
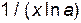
C				arcsin a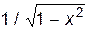
x^n	nx^n- ^1	sin x	cos x	arccos a	–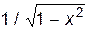
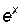
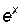
		cos x	-sin x	arctg x	1/(1+ x ^2)
a^x	a^x ln a	tg x	1/cos^2 x	arcctg x	-1/(1+ x ^2)
ln x	1/ x	сtg x	-1/sin^2 x

Приведем основные свойства производной.

1. Если функция имеет производную в точке, то она непрерывна в этой точке.

2. Если существует f¢ (x), и С ‑ произвольное число, то функция 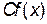имеет производную: (Cf (x)) ¢ = Cf¢ (x).

3. Если существуют f¢ (x)и g¢ (x), то функция S (x) = f (x) + g (x) имеет производную: S¢ (x) = f¢ (x) + g¢ (x).

4. Если существуют f¢ (x) и g¢ (x), то функция P (x) = f (x) g (x) имеет производную: P¢ (x) = f¢ (x) g (x) + f (x) g¢ (x).

5. Если существуют f¢ (x) и g¢ (x) и при этом g (x) ¹ 0, то функция D (x) = f (x) / g (x) имеет производную: D¢ (x) = (f¢ (x) g (x) - f (x) g¢ (x)) / g ²(x).

В любом курсе математического анализа доказывается теорема о производной сложной функции. Мы ограничимся лишь ее формулировкой.

Пусть функция g (x) имеет производную в точке x, а функция f (z) имеет производную в точке z = g (x). Тогда сложная функция F (x) = f (g(x))имеет в точке x производную F¢ (x) = f¢ (z) g ¢ (x).

Приведем примеры вычисления производной сложной функции.

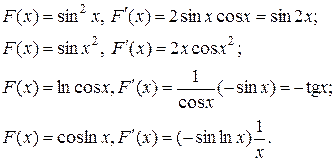
Дата добавления: 2013-12-13