
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Выпуклость и вогнутость функции
|
|
|
|
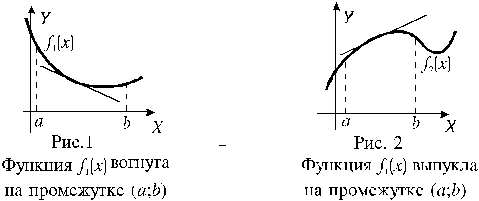
Пусть функция f (x) имеет производную в каждой точке промежутка (a; b). Если на промежутке (a;b) график функции f(x) расположен выше любой своей касательной, проведенной в точке этого промежутка, то функция называется вогнутой на этом промежутке (иногда говорят "выпуклой вниз").
Если на промежутке (a;b) график функции f(x) расположен ниже любой своей касательной, проведенной в точке этого промежутка, то функция называется выпуклой на этом промежутке (иногда говорят "выпуклой вверх").
Точка x0 называется точкой перегиба функции f(x), если в этой точке функция имеет производную и существуют два промежутка: (a;x0) и (x0;b), на одном из которых функция выпукла, а на другом вогнута.
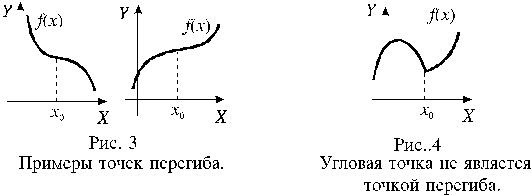
Будем называть функцию возрастающей в точке x0, если она непрерывна в этой точке и возрастает в некоторой ее окрестности. Подобным образом можно определить функцию, убывающую в точке.
Приведем без доказательства важную для исследования функций теорему.
Если  f¢¢ (x) > 0 на промежутке (a; b), то на этом промежутке функция f (x) вогнута. Если f¢¢ (x) < 0 на промежутке (a; b), то на этом промежутке функция f (x) выпукла.
f¢¢ (x) > 0 на промежутке (a; b), то на этом промежутке функция f (x) вогнута. Если f¢¢ (x) < 0 на промежутке (a; b), то на этом промежутке функция f (x) выпукла.
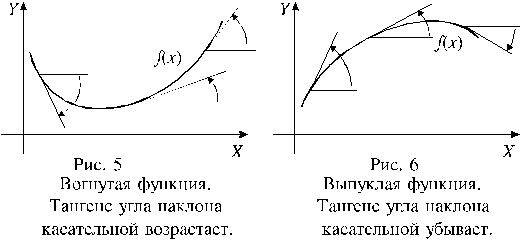
Из положительности второй производной функции на промежутке следует возрастание первой производной на этом промежутке, а это, как показано на рисунке 5, – признак вогнутой функции. Аналогичным образом иллюстрируется второе утверждение теоремы.
Если x 0 – точка перегиба функции f (x), то f¢¢ (x 0) = 0.
Приведем другую формулировку достаточных условий экстремума функции.
Если в точке x 0 выполняются условия:
1) f¢ (x 0) = 0; f¢¢ (x 0) < 0, тогда x 0 – точка максимума;
2) f¢ (x 0) = 0; f¢¢ (x 0) > 0, тогда x 0 – точка минимума;
3) f¢ (x 0) = 0; f¢¢ (x 0) = 0, тогда вопрос о поведении функции в точке остается открытым. Здесь может быть экстремум, например в точке x 0 = 0 у функции y = x 4, но может его не быть, например в точке x 0 = 0 у функции y = x 5. В этом случае для решения вопроса о наличии экстремума в стационарной точке можно использовать достаточные условия экстремума, приведенные выше.
Рассмотрим пример из микроэкономики.
В количественной теории полезности предполагается, что потребитель может дать количественную оценку (в некоторых единицах измерения) полезности любого количества потребляемого им товара.
Это означает существование функции полезности TU аргумента Q – количества купленного товара. Введём понятие предельной полезности, как добавочной полезности, прибавляемой каждой последней порцией товара. Далее построим двумерную систему координат, откладывая по горизонтальной оси
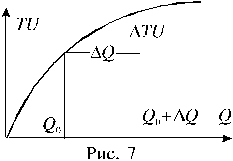
|
количество потребляемого товара Q, а по вертикальной оси – общую полезность TU, как это сделано на рисунке 7. В этой системе координат проведем график функции TU = TU (Q). Точка Q 0 на горизонтальной оси означает количество приобретенного товара, величина D Q –добавочный приобретенный товар. Разность D TU = TU (Q 0 + D Q) – TU (Q 0) ‑ добавочная полезность, полученная от покупки “довеска” D Q. Тогда добавочная полезность от последней приобретенной порции (или единицы количества) товара вычисляется по формуле D TU / D Q (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 122). Эта дробь, как можно видеть, зависит от величины D Q. Если здесь перейти к пределу при D Q ® 0, то получится формула для определения предельной полезности MU:
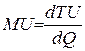 .
.
Это означает, что предельная полезность равна производной функции полезности TU(Q). Закон убывающей предельной полезности сводится к уменьшению этой производной с ростом величины Q. Отсюда следует выпуклость графика функции TU (Q). Понятие функции полезности и представление предельной полезности в виде производной этой функции широко используется в математической экономике.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 371; Нарушение авторских прав?; Мы поможем в написании вашей работы!