Дифференциал функции. Рассмотрим две функции: y1 = f1(x) и y2 = f2(x), которые имеют производные f1¢ (x) и f2¢ (x) в каждой точке некоторой области D

Рассмотрим две функции: y ₁ = f ₁(x) и y ₂ = f ₂(x), которые имеют производные f ₁ ¢ (x) и f ₂ ¢ (x) в каждой точке некоторой области D. Возьмем какую-либо точку x из области D и дадим аргументу приращение D x. Тогда функции получат соответственно приращения D y ₁ = f ₁(x + D x) - f ₁(x) и D y ₂ = f ₂(x + D x) - f ₂(x). Из графиков, изображенных на рисунке 3, видно, что в обоих случаях приращения D y ₁ и D y ₂ можно представить в виде сумм двух слагаемых:

D y ₁ = (C ₁ - A ₁) + (B ₁ - C ₁); D y ₂ = (C ₂ - A ₂) + (B ₂ - C ₂) (1)

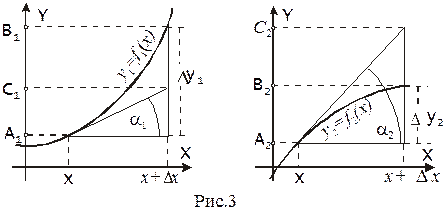
Первые слагаемые в правых частях обоих выражений (1) легко вычисляются из сходных формул: C ₁ – A ₁ = tg a ₁ D x = f ₁ ¢ (x)D x; C ₂ – A ₂ = tg a ₂ D x = f ₂ ¢ (x)D x.

Величина f¢ (x) D x называется главной частью приращения функции y = f (x) в точке x. (Здесь мы говорим только о функции, имеющей в точке x производную). Главная часть приращения функции линейна относительно приращения аргумента D x (можно сказать – пропорциональна приращению D x). Это означает, что если приращение аргумента D x уменьшить в k раз, то и главная часть приращения функции уменьшится в k раз.

Формулы (1) можно переписать в виде:

D y ₁ = f ₁ ¢ D x + r ₁; Dy ₂ = f ₂ ¢ D x + r ₂. (2)

Здесь r ₁ = B ₁ – C ₁; r ₂= B ₂– C ₂.

Величины r ₁ и r ₂ в формулах (2) при уменьшении D x в k раз уменьшаются более чем в k раз, что можно видеть, сравнивая рисунки 3 и 4, и говорят, что r ₁ и r ₂ стремятся к нулю быстрее, чем D x.

Назовем функцию b(z) бесконечно малой в точке z = z ₀, если .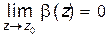

Пусть функции b(z)и g (z)являются бесконечно малыми в точке z = z ₀.. Функция b (z) называется бесконечно малой более высокого порядка, чем функция g (z), если .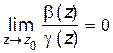

Величины r ₁ и r ₂ в формулах (2) являются функциями аргумента D x, бесконечно малыми в точке D x = 0. Можно показать, что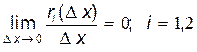. Это означает, что функции r ₁(Dx) и r ₂(D x) являются бесконечно малыми функциями более высокого порядка, чемD x, в точкеD x = 0.

Таким образом, приращение функции y = f (x)в точке, в которой существует её производная, может быть представлено в виде

D y = f¢ (x) D x + b(D x),

где b(D x) ‑ бесконечно малая функция более высокого порядка, чем D x, в точке D x = 0.

Главная, линейная относительно D x, часть приращения функции y = f (x), равная f¢ (x) D x, называется дифференциалом и обозначается dy:

dy = f¢ (x) D x. (3)

Если сюда подставить функцию f (x) = x, то, так как x¢ = 1, формула (3) примет вид: dx = D x. Эта формула легко истолковывается с помощью графика функции y = x, из которого видно, что приращение этой функции содержит лишь главную часть. Таким образом, для функции y = x приращение совпадает с дифференциалом. Теперь формулу дифференциала (3) можно переписать так

dy = f¢ (x) dx.

Отсюда следует, что

,

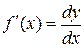то есть производная функции f(x) равна отношению дифференциала функции к дифференциалу аргумента x.

Очевидны следующие свойства дифференциала.

1. dC = 0 (здесь и в следующей формуле C - постоянная);

2. d (Cf (x)) = Cdf (x);

3. Если существуют df (x) и dg (x), то d (f (x) + g (x)) = df (x) + dg (x), d (f (x) g (x)) = g (x) df (x) + f (x) dg (x). Если при этом g (x) ¹0, то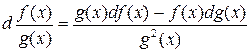

Пусть y = f (x) ‑ функция, имеющая производную в точке x, тогда dy = df (x) = f¢ (x) dx. Если аргумент x является функцией x (t) некоторой независимой переменной t, то y = F (t) = f (x (t)) -сложная функция от t, и её дифференциал вычисляется по формуле dy = F¢ (t) dt = f¢ (x) x¢ (t) dt. Однако по определению дифференциала x¢ (t) dt = dx и последняя формула преобразуется к виду: dy = f¢ (x) dx.

Таким образом, если аргумент функции y=f (x)рассматривать как функцию другого аргумента так, что равенство D x = dx не выполняется, формула дифференциала функции f (x) остается неизменной. Это свойство принято называть свойством инвариантности дифференциала.

Дата добавления: 2013-12-13