Частные производные

Функция нескольких переменных. Основные понятия

Пусть имеется (n +1) переменная x ₁, x ₂,..., x _n, y, которые связаны между собой так, что каждому набору числовых значений переменных x ₁, x ₂,..., x_n соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x ₁, x ₂,..., x_n называется значением функции f в точке (x ₁, x ₂,..., x_n), что записывается в виде формулы y = f (x ₁ ,x ₂,..., x_n) или y = y (x ₁ ,x ₂,..., x_n).

Переменные x ₁, x ₂,..., x_n являются аргументами этой функции, а переменная y ‑ функцией от n переменных.

Далее будем говорить лишь о функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны, или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать, как правило, x и y, а значение функции - z.

Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f (x,y) и называется значением функции f в точке (x,y).

Множество D называется областью определения функции.

Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f (x,y) можно писать z = f (M). При этом аргументами функции будут координаты x и y точки M.

График функции двух переменных есть множество точек (x, y, f (x, y)), где (x,y)Î D. График представляет собой некоторую поверхность. Пример такой поверхности приводится на Рис. 1.

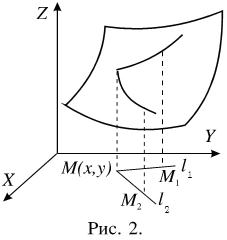Очевидно, что нельзя ввести понятия возрастания или убывания (монотонности) функции двух переменных. Рассмотрим график некоторой функции z = f (x,y), изображенный на Рис. 2. Из точки M (x,y) в плоскости X,Y проведем два луча l ₁ и l ₂, определяющих некоторые направления. Можно говорить, что в точке M функция f в направлении l ₁ возрастает, а в направлении l ₂ убывает. Это означает, что для любой точки M ₁, лежащей на луче l ₁ достаточно близко к точке M, выполняется неравенство f (M ₁) > f (M). Для любой точки M ₂ , лежащей на луче l ₂ достаточно близко к точке M, выполняется неравенство f (M ₂) < f (M).

Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.

Можно использовать другой подход. Пусть имеется функция z = f (x, y) c графиком, представляющим собой некоторую поверхность.

Рассмотрим сечение графика функции плоскостью z=C (эта плоскость параллельна плоскости XOY и пересекает ось Z в точке z=C). Спроектируем линию пересечения этой плоскости с поверхностью z = f (x, y) на плоскость XOY и получим так называемую линию уровня C функции z = f (x, y). Линия уровня представляет собой множество всех точек в плоскости XOY, для которых выполняется равенство f (x, y) = C. Придавая различные значения параметру C, можно получить множество линий уровня функции f (x, y). Если для каждой линии уровня указать соответствующее ей значение C, то получится топографическая карта поверхности, представляющей собой график функции.

В микроэкономике, в предположении, что потребитель приобретает лишь два вида товаров: A и B, вводится понятие общей полезности TU, как функции двух аргументов: Q ₁ и Q ₂ – количеств потребленных товаров A и B, соответственно:

TU = TU (Q ₁, Q ₂). (1)

Очевидно, что все линии уровня функции TU (Q ₁, Q ₂) составляют семейство кривых безразличия (Курс экономической теории. Под общей редакцией проф. Чепурина М.Н. 1995, стр. 125).

Пусть в плоскости XOY заданы две точки: M ₀(x ₀, y ₀) и M ₁(x ₁, y ₁). Расстояние r между этими точками рассчитывается по формуле

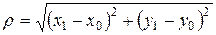. (2)

Пусть d ‑ некоторое положительное число. d - окрестностью V_d точки M ₀(x ₀, y ₀) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам

.

Очевидно, что d -окрестность точки M ₀(x ₀, y ₀) представляет собой круг радиуса d с выколотым центром.

Точка M ₀(x ₀, y ₀) называется точкой минимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î V_d (x ₀, y ₀) следует f (x, y) > f (x ₀, y ₀).

Точка M ₀(x ₀, y ₀) называется точкой максимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î V_d (x ₀, y ₀) следует: f (x, y) < f (x ₀, y ₀).

Точки минимума и максимума называются точками экстремума.

Число A называется пределом функцииz = f (x, y) в точкеM ₀(x ₀, y ₀):

,

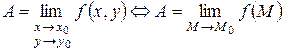если для произвольного числа e > 0 найдется такое число d > 0, что для всех точек M(x,y) из d-окрестности точки M₀(x₀,y₀) выполняется неравенство

| f (x, y) - A |< e.

Функция z = f (x, y) называется непрерывной в точкеM ₀(x ₀, y ₀), если

.

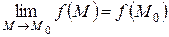Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной.

Частной производной поx функцииz = f (x, y) в точкеM ₀(x ₀, y ₀) называется предел

,

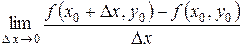если этот предел существует. Обозначается эта частная производная любым из следующих символов:

;;.

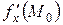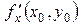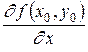Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.

Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точкеM ₀(x ₀, y ₀):

=.

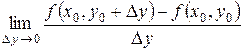В пространстве XYZ условие y = y ₀ описывает плоскость P, перпендикулярную оси OY и пересекающую эту ось в точке y ₀. Плоскость P пересекается с графиком функции z = f (x, y), вдоль некоторой линии L, как показано на рисунке 1. Тангенс угла между плоскостью XOY и касательной к линии L в точке с координатами x ₀, y ₀ равен частной производной по x функции z = f (x, y)в этой точке. В этом состоит геометрический смысл частной производной.

Аналогичное заключение можно сделать относительно частной производной по y.

Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f (x, y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.

Примеры. 1. .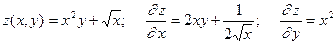

2.

Если частные производные функции z = f (x, y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:

.

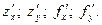Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называются вторыми частными производными или частными производными второго порядка и обозначаются z_xx ¢¢, z_yy¢¢, z_xy¢¢ или . Согласно определению 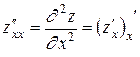; . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная z_xy¢¢ = (z_x¢) _y¢ может не быть равной z_yx¢¢ = (z_y¢) _x¢. Однако существует теорема, утверждающая, что если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y.

Пример. Рассмотрим функцию 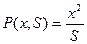, где x — численность в городах, S — расстояние между городами, P — пассажиропоток. Тогда — при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей: ; 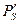— при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами: .

Дата добавления: 2013-12-13