
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неопределенный интеграл. Функция F(x) называется первообразной для функции f(x) на промежутке (a;b), если для всех xÎ(a;b) выполняется равенство F¢(x) = f(x)
|
|
|
|
Функция F (x) называется первообразной для функции f (x) на промежутке (a; b), если для всех xÎ(a; b) выполняется равенство F¢ (x) = f (x).
Например, для функций
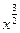 первообразной будет функция
первообразной будет функция 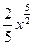 ,
,
sin3x 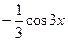
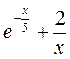
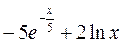
Если для F (x) установлено равенство dF (x) = f (x) dx, то F (x) ¾ первообразная для f (x), так как  .
.
Рассмотрим две теоремы, которые называются теоремами об общем виде всех первообразных данной функции.
Теорема 1. Если F(x) – первообразная для f (x) на (a; b), то F (x) + C, где C – число, тоже первообразная для f (x) на (a; b).
Доказательство.
(F + C) ¢ = F¢ + C¢ = f + 0 = f
По определению F + C ¾ первообразная для f.
Прежде чем рассмотреть теорему 2, докажем две вспомогательные теоремы.
Если функция g (x) постоянна на (a; b), то g¢ (x) = 0.
Доказательство.
Так как g (x) = C, справедливы равенства: g¢ (x) = C¢ = 0.
Если g¢ (x) = 0 при всех x Î(a; b), то g (x) = C на (a; b).
Доказательство.
Пусть g¢ (x) = 0 во всех точках (a; b). Зафиксируем точку x 1Î(a; b). Тогда для любой точки x Î(a; b) по формуле Лагранжа имеем
g (x) – g (x 1) = g¢ (x)(x – x 1)
Так как x Î(x; x 1), а точки x и x 1 принадлежат промежутку (a; b), то g¢ (x) = 0, откуда следует, что g (x) – g (x 1)=0, то есть g (x) = g (x 1)= const.
Теорема 2. Если F (x) есть первообразная для f (x) на промежутке (a; b), а G (x) – другая первообразная для f (x) на (a; b), то G = F + C, где C – число.
Доказательство.
Возьмем производную от разности G – F: (G – F) ¢ = G¢ – F¢ =
= f – f = 0. Отсюда следует: G – F = C, где C ¾ число, то есть G = F + C.
Множество всех первообразных для функции f (x) на промежутке (a; b) называется неопределенным интегралом от f (x) и обозначается ò f (x) dx. f (x) dx ¾ подинтегральное выражение, f (x) ¾ подинтегральная функция. Если F(x) – первообразная для f(x), то ò f(x)dx = F(x) + C, где C – произвольное число.
Вычисление неопределенного интеграла от заданной функции называется интегрированием.
Из определения неопределенного интеграла следует, что каждой формуле дифференциального исчисления F¢ (x) = f (x) соответствует формула ò f (x) dx = F (x) + C интегрального исчисления. Отсюда получается таблица неопределенных интегралов:
| 1) ò dx = x + C; | 7) ò cos x dx = sin x + C; |
2) ò xndx = 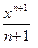 + C, (n ¹ –1); + C, (n ¹ –1);
| 8) 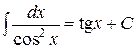 ; ;
|
3) 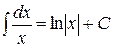 ; ;
| 9) 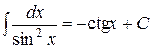 ; ;
|
| 4) ò exdx = ex + C; | 10) 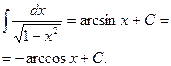
|
5) ò axdx = 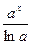 + C; + C;
| 11) 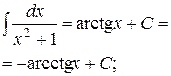
|
| 6) ò sin x dx = -cos x + C; |
Т.е. взяли таблицу производных, прочитали её «задом наперёд» и получили таблицу интегралов.
По постановке задачи
| Дифференцирование | Интегрирование |
| Задана функция f (x). Требуется найти производную f¢ (x). | Задана функция F (x), являющаяся производной функции f (x). Требуется найти функцию f (x). |
Итак, интегрирование — это операция обратная дифференцированию.
Неопределенный интеграл обладает следующими свойствами:
| 1) (ò f (x) dx) ¢=f (x); | 4) ò d f (x)= f (x)+ C; |
| 2) ò f¢ (x) dx = f (x)+ C; | 5) ò kf (x) dx=k ò f (x) dx; |
| 3) d ò f (x) dx= f (x) dx; | 6) ò (f (x)+ g (x)) dx= ò f (x) dx +ò g (x) dx; |
7) Если ò f (x) dx = F (x) + C, то ò f (ax+b) dx = 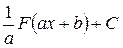 (a ¹ 0).
(a ¹ 0).
|
Все эти свойства непосредственно следуют из определения.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 749; Нарушение авторских прав?; Мы поможем в написании вашей работы!