
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 2. Алгебра логики (Булева алгебра)
|
|
|
|
Алгебра логики (Булева алгебра)
Что такое алгебра? Что такое булева алгебра? (См. Математический энциклопедический словарь)
А,В,С,... – высказывания.
Операции над высказываниями:
отрицание (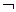 ), конъюнкция (
), конъюнкция ( ), дизъюнкция (
), дизъюнкция (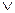 ), импликация (
), импликация (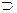 ), эквивалентность (
), эквивалентность (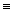 ).
).
Истинностные таблицы:
| A | B | 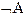
| 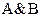
| 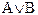
| 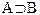
| 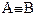
|
| и | и | л | и | и | и | и |
| и | л | л | л | и | л | л |
| л | и | и | л | и | и | л |
| л | л | и | л | л | и | и |
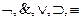 - пропозициональные связки.
- пропозициональные связки.
А,В,С,... - пропозициональные буквы (переменные).
Определение:
1. Все пропозициональные буквы являются пропозициональными формами.
2. Если 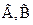 - пропозициональные формы, то
- пропозициональные формы, то 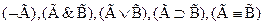 - тоже пропозициональные формы.
- тоже пропозициональные формы.
Каждому распределению истинностных значений пропозициональных переменных, входящих в пропозициональную форму, соответствует некоторое истинностное значение пропозициональной формы. Каждой пропозициональной форме можно сопоставить истинностную таблицу.
Пример: Истинностная таблица для формы 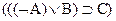
| А | В | С | 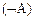
| 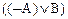
| 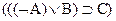
|
| и | и | и | л | и | и |
| л | и | и | и | и | и |
| и | л | и | л | л | и |
| л | л | и | и | и | и |
| и | и | л | л | и | л |
| л | и | л | и | и | л |
| и | л | л | л | л | и |
| л | л | л | и | и | л |
Определения:
Тавтология - истинностная форма, которая при любых значениях пропозициональных переменных принимает значение «и».
Противоречие - истинностная форма, которая при любых значениях пропозициональных переменных принимает значение «л».
Если 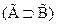 - тавтология, то говорят, что
- тавтология, то говорят, что 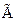 логически влечет
логически влечет 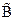 (или
(или 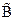 является логическим следствием
является логическим следствием 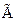 ). Если
). Если 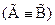 - тавтология, то говорят, что
- тавтология, то говорят, что 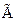 и
и 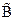 логически эквивалентны.
логически эквивалентны.
Доказать: Истинностная форма 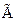 тавтология тогда и только тогда, когда
тавтология тогда и только тогда, когда 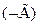 - противоречие.
- противоречие.
Примеры тавтологий:
1. 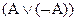 - закон исключенного третьего;
- закон исключенного третьего;
2. 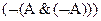 ;
;
3. 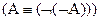 ;
;
4. 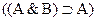 ;
;
5. 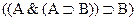 ;
;
6. 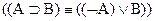 .
.
В естественном языке или в формальной теории тавтологии соответствуют логически истинным высказываниям, а противоречия – логически ложным высказываниям.
Доказать: Если 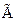 и
и 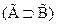 - тавтологии, то и
- тавтологии, то и 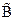 - тавтология.
- тавтология.
Договоренности:
* Опускать внешние скобки у пропозициональных форм;
* Если 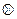 - пропозициональная связка, то
- пропозициональная связка, то 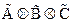 понимается как
понимается как 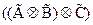 ;
;
* Связки упорядочены по возрастанию старшинства так: 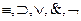
Например:
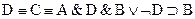 означает
означает 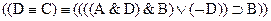 .
.
Упражнения:
Исключить возможно большее число скобок в формах:
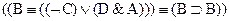

Восстановить скобки в формах:
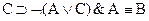
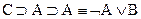
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 361; Нарушение авторских прав?; Мы поможем в написании вашей работы!