Конечный автомат

Конечный автомат А=<V,Q,d,q₀,F>, где

V={a₁,a₂,..,a_m} - входной алфавит;

Q={q₀,q₁,...,q_n-1} - алфавит состояний;

d: Q´V®Q - функция переходов;

q₀ÎQ - начальное состояние;

FÍQ - множество заключительных состояний.

На ленте слово из V. Устройство чтения находится в начальном состоянии против первого символа. Устройство чтения за один такт перемещается на одну позицию вправо и изменяет свое состояние в соответствии с функцией перехода. Если пара (q_i,a_j), характеризующая состояние автомата, не является левой частью функции переходов, то автомат останавливается. Цепочка допускается конечным автоматом, если устройство чтения прочитывает последний символ и оказывается в одном из заключительных состояний.

Для каждой автоматной грамматики можно построить конечный автомат, распознающий слова языка.

Каждому конечному автомату можно сопоставить порождающую грамматику для множества допустимых цепочек.

Автоматная грамматика Û Конечный автомат

Пусть задана регулярная грамматика G=<N,T,P,S>, с правилами вида A®aB или C®b.

Конечный автомат A=<V,Q,d,q₀,F> допускает язык, порождаемый G, если

1). V=T;

2). Q=NÈ{Z}, где ZÏN, ZÏT;

3). q₀=S;

4). F={Z};

5). Отображение d: для правил вида A®aB команда (A,a) ®B, для правил вида C®b команда (C,b) ®Z

Пример:

Регулярная грамматика, порождающая идентификаторы G=<N,T,P,S>	Автомат, распознающий идентификаторы A=<V,Q,d,q0,F>
N={I,K}, T={б,ц}, S=I, P={1. I®б, 2. I®бK, 3. K®бK, 4. K®цK, 5. K®б, 6. K®ц}	V=T={б,ц}; Q=NÈ{Z}={I,K,Z}; q0=S=I; F={Z}; d: {1. (I,б) ®Z, 2. (I,б)®K, 3. (K,б)®K, 4. (K,ц)®K, 5. (K,б) ®Z, 6. (K,ц) ®Z }

Совокупность команд может быть представлена диаграммой состояний:

Различают недетерминированный конечный автомат (НДКА) и детерминированный (ДКА). НДКА на диаграмме состояний имеет вершину, из которой выходит несколько дуг с одинаковыми пометками. Классы языков, допускаемых НДКА и ДКА совпадают. Вот эквивалентный ДКА для нашего примера:

Проверяемое слово дополнено в конце еще одним символом - символом конца слова.

В практических целях необходимо обеспечить единообразие завершения обработки лексемы автоматом не зависимо от того, принята или не цепочка. Для этого вводят еще два состояния: О - была ошибка во входной цепочке; конечное состояние Е - цепочка отвергнута. Вот как будет выглядеть диаграмма состояний:

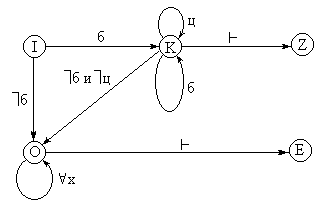
Порядок конструирования лексического анализатора:

1). Выделить во входном языке L(G) множество классов лексем - L_i, 1<=i<=k, k>=1.

2). Для каждого класса лексем L_i построить автоматную грамматику G_i, порождающую язык L_i.

3). Для каждой автоматной грамматики G_i построить диаграмму состояний (неформальная модель распознавателя).

4). Выбрать формат и код образов лексем - дескрипторов.

5). Запрограммировать распознаватель по склеенной диаграмме переходов.

Дата добавления: 2013-12-13