Контекстно - свободные грамматики

Синтаксический анализ

Конечный автомат

Регулярные языки

Порождающая грамматика G=<N,T,P,S>, правила которой имеют вид: A®aB или C®b, где A,B,CÎN, a,bÎT называется регулярной (автоматной).

Язык, порождаемый автоматной грамматикой, называется автоматным (регулярным), или языком с конечным числом состояний.

Конечный автомат А=<V,Q,d,q₀,F>, где

V={a₁,a₂,..,a_m} - входной алфавит; Q={q₀,q₁,...,q_n-1} - алфавит состояний;

d: Q´V®Q - функция переходов; q₀ÎQ - начальное состояние;

FÍQ - множество заключительных состояний.

На ленте слово из V. Устройство чтения находится в начальном состоянии против первого символа.

Устройство чтения за один такт перемещается на одну позицию вправо и изменяет свое состояние в соответствии с функцией перехода.

Если пара (q_i,a_j), характеризующая состояние автомата, не является левой частью функции переходов, то автомат останавливается. Цепочка допускается конечным автоматом, если устройство чтения прочитывает последний символ и оказывается в одном из заключительных состояний.

Автоматная грамматика Û Конечный автомат

Пусть задана регулярная грамматика G=<N,T,P,S>, с правилами вида A®aB или C®b.

Конечный автомат A=<V,Q,d,q₀,F> допускает язык, порождаемый G, если

1). V=T;

2). Q=NÈ{Z}, где ZÏN, ZÏT;

3). q₀=S;

4). F={Z};

5). Отображение d: для правил вида A®aB команда (A,a) ®B, для правил вида C®b команда (C,b) ®Z

Продукции имеют вид А®b, где А - нетерминал, bÎV*=(TUN)*.

Вывод неоднозначен, поэтому вводят термин «левосторонний» («правосторонний») - вывод, когда правило вывода применяется к самому левому (правому) вхождению нетерминального символа.

Пример 1. G=<N,T,P,S>, где N={E}, T={i,+,*}, S=E, P={E®E+E |E*E |i}, i - идентификатор.

Эта грамматика порождает арифметические выражения без скобок с операциями сложения и умножения.

Цепочка i+i*i может быть выведена так (левосторонний вывод):

E®E+E®i+E®i+E*E®i+i*E®i+i*i; a).

E®E*E®E+E*E®i+E*E®i+i*E®i+i*i; b).

Удобнее представлять вывод с помощью дерева синтаксического разбора:

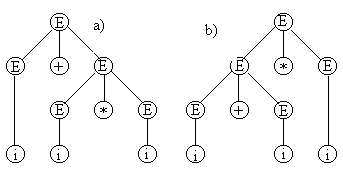
КС-грамматика называется неоднозначной, если для некоторой цепочки существует несколько деревьев синтаксического разбора.

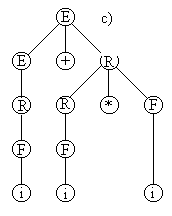
Пример 2. G=<N,T,P,S>, где N={E,R,F}, T={i,+,*,(,)}, S=E, P={E®E+R | R, R®R*F |F, F®(E) |i}, i - идентификатор.

Единственный левосторонний вывод цепочки i+i*i и единственное дерево синтаксического разбора: c).

Имеется математический аппарат преобразования КС-грамматик, сохраняющий способность порождать тот же язык, что и исходная грамматика. Прежде чем строить распознающий алгоритм, КС-грамматику преобразуют, добиваясь необходимых свойств.

КС-грамматика имеет нормальную форму Грейбах, если все порождающие правила в ней имеют вид А®ba, где А - нетерминал, b - терминал, aÎN*.

Дата добавления: 2013-12-13