Случайное событие. Вероятность

Детерминированные и стохастические принципы в физических методах исследования биологических систем и объектов

В теории вероятностей исследуются закономерности, относя­щиеся к случайным событиям, величинам, процессам. Врачи редко задумываются, что постановка диагноза имеет вероятно­стный характер и, как остроумно замечено, лишь патологоана-томическое исследование может достоверно определить ди­агноз умершего человека.

Наблюдая различные явления, можно заметить, что существу­ет два типа связей между условиями S и наступлением или ненас­туплением некоторого события А. В одних случаях осуществление комплекса условий S (испытание) непременно вызывает событие А. В других случаях многократное повторение испытания может привести или не привести к появлению события А. Такие события принято называть случайными: к ним можно отнести появление в кабинете врача больного с данной болезнью, выпадение опреде­ленной стороны монеты при ее бросании и др.

Не следует думать о случайных явлениях как о беспричинных, ничем не обусловленных. Известно, что многие явления связаны между собой, отдельное явление представляет следствие како­го-то другого и само служит причиной последующего. Однако проследить количественно эту связь между условиями и событи­ем часто затруднительно или даже невозможно.

В быту применительно к таким случайным событиям употреб­ляют слова «возможно», «вероятно», «маловероятно», «невероятно».

Однако и случайные события, если их чис­ло достаточно велико, подчиняются определенным закономернос­тям. Количественная оценка закономерностей, относящихся к случайным событиям, дается в разделе математики, называемом теорией вероятностей ..

Теория вероятностей изучает закономерности, присущие мас­совым (статистическим) случайным событиям.

Исторически теория вероятностей появи­лась в связи с попытками подсчета возможности различных исхо­дов в азартных играх. В настоящее же время она применяется в науке, в том числе биологии и медицине, для оценки вероятности практически важных событий. От игр остались лишь наглядные примеры, которые удобно использовать для иллюстрации теоре­тических положений.

Статистическое определение вероятности. Вероятность Р(А) в теории вероятностей выступает как числовая характеристика сте­пени возможности появления какого-либо определенного случай­ного события А при многократном повторении испытаний.

Допустим, при 1000 бросаний игральной кости цифра 4 выпа­дает 160 раз. Отношение 160/1000 = 0,16 показывает относитель­ную частоту выпадания цифры 4 в данной серии испытаний. В бо­лее общем случае, когда случайное событие А происходит т раз в серии п независимых испытаний, относительной частотой со­бытия в данной серии испытаний или просто частотой события А называют отношение

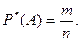(1)

При большом числе испытаний частота события примерно по­стоянна: увеличение числа испытаний уменьшает колебание час­тоты события около постоянной величины.

Вероятностью случайного события назовем предел, к ко­торому стремится частота события при неограниченном увеличении числа испытаний:

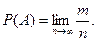(2)

Это статистическое определение вероятности.

Практически за вероятность [см. (2.2)] можно принять относительную частоту события при боль­шом числе испытаний. Так, например, из статистических законо­мерностей рождения, установленных за много лет наблюдений, вероятность того события, что новорожденный будет мальчиком, оценивают в 0,515.

Классическое определение вероятности. Если при испыта­ниях нет каких-либо причин, вследствие которых одно случайное событие появлялось бы чаще других (равновозможные собы­тия), можно определить вероятность исходя из теоретических со­ображений.

Допустим, что в результате испытания должно произойти только одно из п равновозможных несовместных событий (несов­местными называют события, если их одновременное осуществ­ление невозможно). Пусть рассматриваемое событие А происхо­дит в т случаях, которые называются благоприятствующими А, и не происходит при остальных п — т, неблагоприятствующих А. Тогда вероятностью можно назвать отношение благоприят­ствующих случаев к общему числу равновозможных несов­ местных событий:

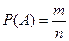(3)

Это классическое определение вероятности. Рассмотрим пример.

* В урне находится 40 шаров: 10 черных и 30 белых. Найти вероят­ность того, что вынутый наугад один шар будет черным.

- Число благоприятствующих случаев равно числу черных шаров в урне: т = 10. Общее число равновозможных событий (вынимание одного шара) равно полному числу шаров в урне: п = 40. Эти события несовмест­ны, так как вынимается один и только один шар. По формуле (3) имеем

Р(А) = 10/40 = 1/4.

В ряде случаев вычислить вероятность события оказывается проще, если представить его в виде комбинации более простых со­бытий. Этой цели служат некоторые теоремы теории вероятнос­тей.

Теорема сложения вероятностей: вероятность появления одного (безразлично какого) события из нескольких несов­местных событий равна сумме их вероятностей. Для двух несовместных событий

Р(А или В) = Р{А) + Р(В). (4)

Докажем эту теорему. Пусть п — общее число испытаний, m₁ — число случаев, благоприятствующих событию А, т₂ — число слу­чаев, благоприятствующих событию В. Число случаев, благопри­ятствующих наступлению либо события А, либо события В, равно m₁ + m₂. Тогда

Отсюда, учитывая (4), имеем

Р(А или В) = Р(А) + Р(В).

Теорема умножения вероятностей: вероятность совместно­го появления независимых событий равна произведению их вероятностей. Для двух событий

Р(А и В) = Р(А) • Р(В). (5)

Докажем эту теорему. Так как события А и В независимы, то каждому из т₁ случаев, благоприятствующих А, соответствуют т₂ случаев, благоприятствующих В. Таким образом, общее число случаев, благоприятствующих совместному появлению событий А и В, равно т₁т₂. Аналогично, общее число равновозможных собы­тий равно n₁n₂, где п₁ и п₂ — числа равновозможных событий со­ответственно для А и В. Имеем

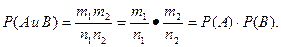(6)

* Найти вероятность того, что в семье с тремя детьми все трое сы­
новья. Считать, что вероятность рождения мальчика равна 0,515 и пол
каждого последующего ребенка не зависит от пола предыдущих детей.

ТПо теореме умножения вероятностей,

Р(А и В и С) = 0,515 • 0,515 • 0,515 ~ 0,14.

Теорема умножения вероятностей усложняется, если оп­ределяется вероятность события, состоящего из совместно­го появления двух зависимых между собой событий. В том случае, когда событие В выполняется при условии, что собы­тие А имело место, вероятность совместного появления двух этих событий равна

Р(АиВ) = Р(А) • Р(В/А), (7)

где Р(В/А) — условная вероятность, т. е. вероятность события В при условии, что событие А состоялось.

Дата добавления: 2013-12-13