Случайная величина. Закон распределения. Числовые характеристики

Определение случайной величины. Многие случайные собы­тия могут быть оценены количественно случайными величинами.

Случайной называют такую величину, которая принима­ет значения в зависимости от стечения случайных обсто­ятельств.

Случайными величинами являются: число больных на приеме у врача, число студентов в аудитории, число рождений в городе, продолжительность жизни отдельного человека, скорость моле­кулы, температура воздуха, погрешность в измерении какой-либо величины и др.

Различают дискретные и непрерывные случайные величины.

Случайная величина называется дискретной, если она принимает счетное множество значений: число букв на произ­вольной странице книги, энергия электрона в атоме, число волос на голове человека, число зерен в колосьях, число молекул в вы­деленном объеме газа и т. п.

Непрерывная случайная величина принимает любые зна­чения внутри некоторого интервала', температура тела, масса зерен в колосьях пшеницы, координата места попадания пули в цель (принимаем пулю за материальную точку) и др.

Распределение дискретной случайной величины. Диск­ретная случайная величина считается заданной, если указаны ее возможные значения и соответствующие им вероятности. Обозна­чим дискретную случайную величину X, ее значения x_1, x₂,..., а вероятности -P(x j) = p₁, P(x₂) = р₂ и т. д. Совокупность X и Р называется распределением дискретной случайной величи­ны (табл. 1).

Таблица 1

X	x1	х2	х3	^Х4	x5	…
р	Pi	Рг	Рз	Pi	Ръ	...

Так как все возможные значения дискретной случайной вели­чины представляют полную систему, то сумма вероят­ностей равна единице:

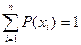. (8)

Здесь предполагается, что дискретная случайная величина имеет п значений. Выражение (8) называется условием норми­ровки.

Числовые характеристики дискретной случайной величи­ны. Во многих случаях, наряду с распределением случайной ве­личины или вместо него, информацию об этих величинах могут дать числовые параметры, получившие название числовых ха­рактеристик случайной величины. Рассмотрим наиболее упот­ребительные из них.

Математическое ожидание (среднее значение) случайной величины есть сумма произведений всех возможных ее значе­ний на вероятности этих значений:

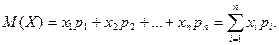(9)

Пусть при большом числе испытаний п дискретная случайная величина X принимает значения x₁ x₂,..., х_п соответственно т₁, т₂,..., т_п раз. Среднее значение равно

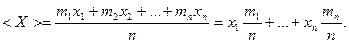
Возможные значения дискретной случайной величины рассеяны вокруг ее математического ожидания, часть из них превышает М(Х), час меньше М(Х). Как оценить степень разброса случайной величины относительно ее среднего значения? Для этого целесообразно учитывать либо абсолютные значения отклонений М [Х - М (X)], либо их квадраты М[Х - М(Х)]². Второй вариант оказывается предпочтительнее, так придем к понятию дисперсии случайной величины.

Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:

D(X) = M[X-M{X)]².

Без вывода приведем удобную для вычисления дисперсии формулу

D(X) = M(X²)-[M{X)]². (10)

Она означает, что дисперсия равна разности между мате: ческим ожиданием квадрата случайной величины X и квадратом ее математического ожидания.

Как следует из (10), дисперсия имеет размерность квадрата размерности случайной величины. Для того чтобы оценивать рас­сеяние случайной величины в единицах той же размерности, вво­дят понятие среднего квадратического отклонения, под кото­рым понимают квадратный корень из дисперсии:

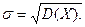(11)

Распределение и характеристики непрерывной случай­ной величины. Непрерывную случайную величину нельзя за­дать тем же законом распределения, что и дискретную. В этом случае поступают следующим образом.

Пусть dP — вероятность того, что непрерывная случайная ве­личина X принимает значения между х и х + dx. Очевидно, что чем больше интервал dx, тем больше и вероятность dP: dP ~ dx. Кроме того, вероятность должна зависеть и от самой случайной величины, вблизи которой расположен интервал, поэтому

dP = f(x)dx, (12)

где f(x) — плотность вероятности, или функция распределе­ ния вероятностей. Она показывает, как изменяется вероят­ность, отнесенная к интервалу dx: случайной величины, в зависи­мости от значения самой этой величины:

f(x) = dP/dx. (13)

Интегрируя выражение (12) в соответствующих пределах, находим вероятность того, что случайная величина принимает ка­кое-либо значение в интервале (аЬ):

Р_аЬ = (14)

Для непрерывной случайной величины математическое ожидание и дисперсия записываются соответственно в виде

Нормальный закон распределения

В теории вероятностей и математической статистике, важную роль играет нормальный закон распределения (закон Гаусса). Случайная величина распределена по этому закону, если плотность вероятности ее имеет вид

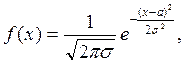
где а = М(Х) — математическое ожидание случайной величины; 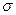— среднее квадратическое отклонение; следовательно, - дисперсия случайной величины.

Кривая нормального закона распределения имеет колоколообразную форму (рис.1), симметричную относительно прямой (центр рассеивания). В точке х = а функция достигает максимума

По мере возрастания \х - а\ функция f(x) монотонно убывает, асимптотически приближаясь к нулю. С уменьшением а кривая становится все более и более островершинной. Изменение а при постоянной 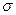не влияет на форму кривой, а лишь сдвигает ее вдоль оси абсцисс. Площадь, заключенная под кривой, согласно условию нормировки, равна единице. На рисунке 1 изображены три кривые. Для кривых 1 и 2 а = 0, эти кривые отличаются зна­чением 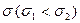кривая 3 имеет а 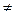0 ().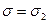

Рис. 1.

Математическая статистика — наука о математических методах систематизации и использования статистических данных для решения научных и практических задач. тематическая статистика тесно примыкает к теории вероятности и базируется на ее понятиях. Однако главным в математической статистике является не распределение случайных величин, а анализ статистических данных и выяснение, какому распределению они соответствуют.

Большая статистическая совокупность, из которой отбирается часть объектов для исследования, называется генеральной совокупностью, а множество объектов, отобранных из нее, — выборочной совокупностью, или выборкой.

Свойство объектов выборки должно соответствовать свойству объектов генеральной совокупности, или, как принято говорить выборка должна быть представительной (репрезентативной) Так, например, если целью является изучение состояния здровья населения большого города, то нельзя воспользоваться боркой населения, проживающего в одном из районов города. Условия проживания в разных районах могут отличаться (различная влажность, наличие предприятий, жилищных строений и.т.п. и, таким образом, влиять на состояние здоровья.

Поэтому выбор­ка должна представлять случайно отобранные объекты. Если записать в последовательности измерений все значения величины х в выборке, то получим простой статистический ряд. Например, рост мужчин (см): 171, 172, 172, 168, 170, 169,.... Та­кой ряд неудобен для анализа, так как в нем нет последователь­ности возрастания (или убывания) значений, встречаются и по­вторяющиеся величины. Поэтому целесообразно ранжировать ряд, например, в возрастающем порядке значений и указать их повторяемость. Получим статистическое распределение выборки:

Здесь x_i — наблюдаемые значения признака (варианта); n_i — число наблюдений варианты х_i (частота); р_i* — относительная частота. Общее число объектов в выборке (объем выборки)

.

всего k вариант.

Статистическое распределение — это совокуп­ность вариант и соответствующих им частот (или относительных частот), т. е. это совокупность данных.

В медицинской литературе статистическое распределение, со­стоящее из вариант и соответствующих им частот, получило на­звание вариационного ряда.

Наряду с дискретным (точечным) статистическим распределе­нием, которое было описано, используют непрерывное (интер­вальное) статистическое распределение.

Интервальная оценка генеральной средней. Точечная оцен­ка, особенно при малой выборке, может значительно отличаться от истинных параметров генеральной совокупности. Поэтому при не­большом объеме выборки пользуются интервальными оценками.

В этом случае указывается интервал (доверительный интер­вал, или доверительные границы), в котором с определенной (до­верительной) вероятностью р находится генеральная средняя.

Интервальная оценка генеральной средней при малой вы­борке. При достаточно большом объеме выборки можно сделать вполне надежные заключения о генеральной средней. Однако на практике часто имеют дело с выборками небольшого объема (п < 30). В этом случае в выражении доверительного интервала точ­ность оценки определяется по следующей формуле:

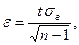
где t — параметр, называемый коэффициентом Стьюдента (его на­ходят из распределения Стьюдента; оно здесь не рассматривает­ся), который зависит не только от доверительной вероятности р, но и от объема выборки п. Коэффициент Стьюдента можно найти из табл. 2.

Таблица 2

Объем выборки, п	Доверительная вероятность, р
0,9	0,95	0,99	0,999
2 3 10	6,31 2,92 1,83 1,76	12,70 4,30 2,26 2,15	63,66 9,93 3,25 2,95	31,60 4,78 4,07

Интервальная оценка истинного значения измеряемой ве­личины. Интервальная оценка генеральной средней может быть ис­пользована для оценки истинного значения измеряемой величины.

Пусть несколько раз измеряют одну и ту же физическую вели­чину. При этом по разным случайным причинам, вообще говоря, получают разные значения: x_v x₂, х₃,.... Будем считать, что нет преобладающего влияния какого-либо фактора на эти измерения.

Истинное значение измеряемой величины (х_ист) совершенно точ­но измерить невозможно хотя бы по причине несовершенства изме­рительных приборов. Однако можно дать интервальную оценку для

этого значения.

Если значения x_v x₂, х₃,... рассматривать как варианты выбор­ки, а истинное значение измеряемой величины х_ист как аналог ге­неральной средней, то можно по описанным выше правилам найти доверительный интервал, в который с доверительной вероятно­стью р попадает истинное значение измеряемой величины. Приме­нительно к малому числу измерений (п < 30) получим:

где — среднее арифметическое значение из полученных измере­ний, а 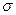— соответствующее им среднее квадратическое отклоне­ние, t — коэффициент Стьюдента.

Более подробно и разносторонне оценка результатов измере­ний рассматривается в практикуме.

Дата добавления: 2013-12-13